
已知函数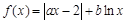 (
(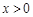 ).
).
(1)若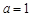 ,
, 在
在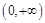 上是单调增函数,求
上是单调增函数,求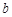 的取值范围;
的取值范围;
(2)若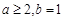 ,求方程
,求方程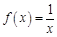 在
在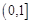 上解的个数.
上解的个数.
(1)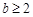 .
.
(2)当a≥3时,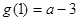 ≥0,∴g(x)=0在
≥0,∴g(x)=0在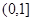 上有惟一解.
上有惟一解.
当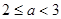 时,
时,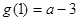 <0,∴g(x)=0在
<0,∴g(x)=0在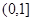 上无解.
上无解.
【解析】(1)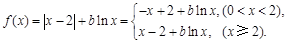 然后分别研究
然后分别研究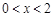 时,
时,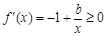 恒成立且
恒成立且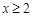 时,
时,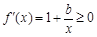 恒成立时b的取值范围即可.
恒成立时b的取值范围即可.
(2) 构造函数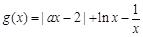 ,即
,即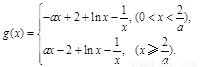
分别研究 和
和 上的单调性,极值和最值.做出草图,数形结合解决即可
上的单调性,极值和最值.做出草图,数形结合解决即可
(1)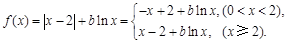 …………………2分
…………………2分
①当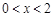 时,
时, 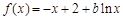 ,
,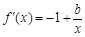 .
.
由条件,得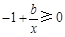 恒成立,即
恒成立,即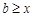 恒成立,∴
恒成立,∴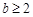 . ……………………4分
. ……………………4分
②当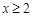 时,
时,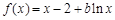 ,
,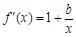 .
.
由条件,得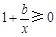 恒成立,即
恒成立,即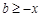 恒成立,∴b≥-2.
恒成立,∴b≥-2.
综合①,②得b的取值范围是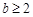 . ……………6分
. ……………6分
(2)令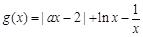 ,即
,即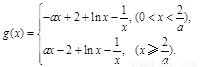 ………………8分
………………8分
当 时,
时,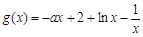 ,.
,.
∵ ,∴
,∴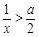 .则
.则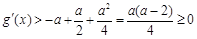 .
.
即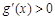 ,∴
,∴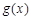 在(0,
在(0,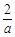 )上是递增函数.………………………10分
)上是递增函数.………………………10分
当 时,
时,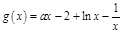 ,
,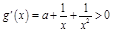 .
.
∴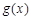 在(
在(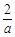 ,+∞)上是递增函数.
,+∞)上是递增函数.
又因为函数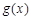 在
在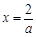 有意义,∴
有意义,∴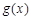 在(0,+∞)上是递增函数.………12分
在(0,+∞)上是递增函数.………12分
∵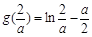 ,而
,而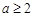 ,∴
,∴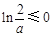 ,则
,则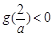 .∵a≥2,
.∵a≥2,
∴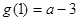 , ……14分
, ……14分
当a≥3时,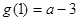 ≥0,∴g(x)=0在
≥0,∴g(x)=0在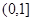 上有惟一解.
上有惟一解.
当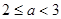 时,
时,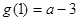 <0,∴g(x)=0在
<0,∴g(x)=0在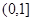 上无解
上无解


科目:高中数学 来源: 题型:
| 1 | 2x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com