甲、乙、丙、丁四名广交会志愿者分在同一组.广交会期间,该组每天提供上午或下午共两个时间段的服务,每个时间段需且仅需一名志愿者.
(1)如果每位志愿者每天仅提供一个时间段的服务,求甲、乙两人在同一天服务的概率;
(2)如果每位志愿者每天可以提供上午或下午的服务,求甲、乙两人在同一天服务的概率.
【答案】
分析:(1)列出甲、乙、丙、丁四名广交会志愿者在同一天的所有服务情况,然后找出甲、乙两人在同一天服务的情况个数求商.
(2)每位志愿者每天可以提供上午或下午的服务是说明一个人可以一天既在上午服务又在下午服务,同样列出所有情况,甲乙在同一天服务的情况不变.
解答:解:(1)从四个人中选出2个人去上午或下午服务(仅一段)是一个基本事件,
基本事件总数有:(甲、乙),(甲、丙),(甲,丁),(乙、甲),(乙、丙),(乙,丁),(丙,甲),(丙,乙),(丙,丁),(丁,甲),(丁,乙),(丁,丙)共12种情况,每种情况的发生都是等可能的,符合古典概型的条件,
其中甲乙在同一天服务有2种情况(乙、甲),(甲、乙),
所以甲.乙两人在同一天服务的概率
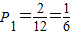
.
(2)从四个人中选出2个人(可以重复选同一个人)去上午或下午服务(一段或两段)是一个基本事件,(甲、甲),(甲、乙),(甲、丙),(甲,丁),(乙、甲),(乙,乙),(乙、丙),(乙,丁),(丙,甲),(丙,乙),(丙,丙),(丙,丁),(丁,甲),(丁,乙),(丁,丙),
(丁,丁)共16种情况每种情况的发生都是等可能的,符合古典概型的条件.
“其中甲乙在同一天服务”有2种情况(甲、乙),(乙、甲).
所以甲.乙两人在同一天服务的概率
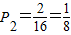
.
点评:本题考查了列举法计算基本事件及事件发生的概率,考查了枚举法,解答的关键是枚举时不重不漏,属中低档题.

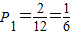 .
.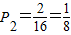 .
.
