
设函数f(x)=4x3+ax2+bx+5在x=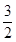 与x=-1时有极值.
与x=-1时有极值.
(1)写出函数的解析式;
(2)指出函数的单调区间;
(3)求f(x)在[-1,2]上的最大值和最小值.
(1) f(x)= 4x3-3x2-18x+5
(2) (-1, )
)
(3) f(x)在[-1,2]上的最小值是-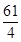 ,最大值为16.
,最大值为16.
【解析】此题主要考查多项式函数的导数,函数单调性的判定,函数最值,函数、方程等基础知识,考查运算求解能力、推理论证能力及分析与解决问题的能力,难度不大.
(1)首先求出函数的导数,然后f′(-1)=0,f′( )=0,解出a、b的值,进而求出解析式
)=0,解出a、b的值,进而求出解析式
(2)f′(x)<0,求出函数的单调区间;
(3)由(1)求出端点处函数值,从而求出函数f(x)在[-1,2]上的最大值和最小值.
解:(1) f
¢(x)=12x2+2ax+b.?由题设知x =  与x =-1时函数有极值.
与x =-1时函数有极值.
则x =  与x =-1满足f ¢(x)=0.
与x =-1满足f ¢(x)=0.
解得a =-3,b =-18. ∴f(x)= 4x3-3x2-18x+5. ……4分
(2)f ¢(x)=12x2-6x-18=6(x+1)(2x-3),
令f ¢(x)>0得:(-∞,-1)和( ,+∞)均为函数的单调递增区间;
,+∞)均为函数的单调递增区间;
(-1, )为函数的单调递减区间. ……8分
)为函数的单调递减区间. ……8分
(3)极值点(-1,  ) 均属于[-1,2],?
) 均属于[-1,2],?
又∵f(-1)=16, f(2)=-11, f( )=-
)=-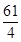 , ……10分
, ……10分
故f(x)在[-1,2]上的最小值是-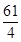 ,最大值为16. ……12分
,最大值为16. ……12分
注:其它解法可酌情给分.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设函数f(x)=x2-4x+3,g(x)=3x-2,集合M={x∈R|f(g(x))>0},N={x∈R|g(x)<2},则M∩N为 ( )
A.(1,+∞) B.(0,1)
C.(-1,1) D.(-∞,1)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖北省武汉市高三11月调考文科数学试卷(解析版) 题型:选择题
设函数f(x)=x3-4x+a,0<a<2.若f(x)的三个零点为x1,x2,x3,且x1<x2<x3,则( )
A.x1>-1 B.x2<0 C.x2>0 D.x3>2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省临海市高三第三次模拟理科数学试卷(解析版) 题型:选择题
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
A.x1>-1 B.x2<0 C.x2>0 D.x3>2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省高二5月第一次周考文科数学试卷(解析版) 题型:选择题
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
A.x1>-1 B.x2<0 C.x2>0 D.x3>2
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省高三第四次(12月)月考文科数学试卷(解析版) 题型:选择题
设函数f (x)=x3-4x+a,0<a<2.若f (x)的三个零点为x1,x2,x3,且x1<x2<x3,则
A.x1>-1 B.x2<0 C.x2>0 D.x3>2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com