练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    １（本小题满分14分）甲、乙两人进行乒乓球单打比赛，采用五局三胜制（即先胜三局者获冠军）．对于每局比赛，甲获胜的概率为，乙获胜的概率为．如果将“乙获得冠军”的事件称为“爆出冷门”．试求此项赛事爆出冷门的概率．


    解析:

    解：如果某方以或获胜，则将未比的一局补上，并不影响比赛结果．于是，问题转化为：求“乙在五局中至少赢三局的概率”．…………（3分）

    乙胜五局的概率为；…（6分）乙胜四局负一局的概率为；……（9分）

    乙胜三局负二局的概率为……（12分）

    以上结果相加，得乙在五局中至少赢三局的概率为………（14分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014届江苏连云港灌南高级中学高二上期中考试文数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    已知：集合集合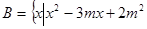

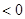
    （１）若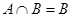，求实数ｍ的取值范围（２）若集合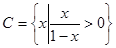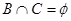，，求实数ｍ的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省苏北四市高三第三次模拟考试数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    在一个半径为1的半球材料中截取三个高度均为h的圆柱，其轴截面如图所示，设三个圆柱体积之和为。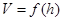

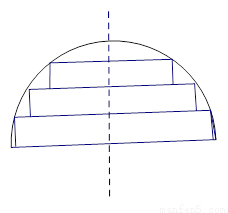
    （１）  求f(h)的表达式，并写出h的取值范围是 ；

    （２）  求三个圆柱体积之和V的最大值；

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年江苏省苏北四市高三第三次模拟考试数学试卷（解析版） 题型：解答题

    （本小题满分14分）

    如图，在直三棱柱ABC-A1B1C1中，已知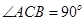，M为A1B与AB１的交点，N为棱B1C1的中点

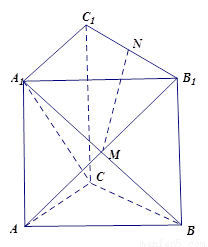
    （１）   求证：MN∥平面AA１C１C

    （２）   若AC＝AA1，求证：MN⊥平面A1BC

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省高三上学期开学考试理科数学卷 题型：解答题

    （本小题满分14分）

    已知函数.

    （１）求函数的单调区间；

    （２）设，求在上的最大值；

    （３）试证明：对任意，不等式恒成立．

     

    查看答案和解析>>

    同步练习册答案