
在 中,若
中,若 。
。
(1)求角 的大小;
的大小;
(2)如果 ,
, ,求
,求 ,
, 的值。
的值。
(1) A=60°.(2)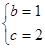 或
或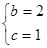
【解析】
试题分析:(1)∵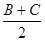 =
=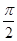 -
-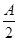 ,
,
∴sin 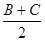 =cos
=cos 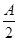 ,
,
∴原式可化为8cos2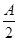 -2cos 2A=7,
-2cos 2A=7,
∴4cos A+4-2(2cos2A-1)=7,
∴4cos2A-4cos A+1=0,解得cos A=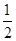 ,∴A=60°.
,∴A=60°.
(2)由余弦定理a2=b2+c2-2bccos A,
∴b2+c2-bc=3.
又∵b+c=3,∴b=3-c,
代入b2+c2-bc=3,并整理得c2-3c+2=0,
解之得c=1或c=2,
∴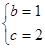 或
或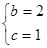
考点:本题主要考查余弦定理的应用,和差倍半的三角函数公式。
点评:中档题,本题解答中,充分利用了函数方程思想,在求交点过程中往往求角的余弦,以避免增解。


科目:高中数学 来源:2012届河北省三河一中高三第二次月考文科数学 题型:解答题
(本题满分12分)
已知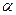 为锐角,且
为锐角,且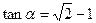 ,函数
,函数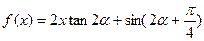 ,数列{
,数列{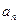 }的首项
}的首项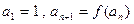 .
.
(1)求函数 的表达式;
的表达式;
(2)在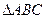 中,若
中,若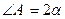 ,
,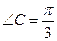 ,BC=2,求
,BC=2,求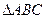 的面积
的面积
(3)求数列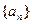 的前
的前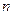 项和
项和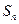 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三第二次月考文科数学 题型:解答题
(本题满分12分)
已知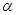 为锐角,且
为锐角,且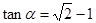 ,函数
,函数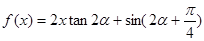 ,数列{
,数列{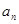 }的首项
}的首项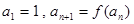 .
.
(1)求函数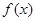 的表达式;
的表达式;
(2)在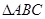 中,若
中,若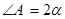 ,
,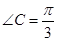 ,BC=2,求
,BC=2,求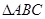 的面积
的面积
(3)求数列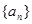 的前
的前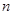 项和
项和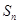 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com