
已知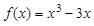 ,并设:
,并设:
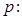
 ,
,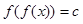 至少有3个实根;
至少有3个实根;
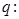 当
当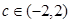 时,方程
时,方程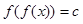 有9个实根;
有9个实根;
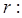 当
当 时,方程
时,方程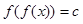 有5个实根.
有5个实根.
则下列命题为真命题的是
A. B.
B. C.仅有
C.仅有 D.
D.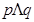
A
【解析】
试题分析:因为,函数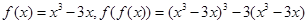
所以,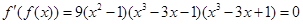 有8个解(4个极大值点,4个极小量值点)
有8个解(4个极大值点,4个极小量值点)
极大值=2,极小值=-2,所以,f(f(x))有9个零点。
令f(f(x))=c,当c>2或c<-2时,f(f(x))=c只有一个实根;
当c=2或c=-2时,f(f(x))=c有5个实根;
当-2<c<-2时,f(f(x))=c有9个实根;
所以P:对于任意的c属于R,f(f(x))=c至少有3个实根;假
q:当c属于(-2,2)时,f(f(x))=c有9个实根;真
r:当c=2时,f(f(x))=c有5个实根;真
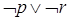 是真命题,故选A。
是真命题,故选A。
考点:本题主要考查函数零点的概念,运用的是研究函数的零点,复合命题真假判断。
点评:中档题,综合性较强,注意理解“函数f(x)的零点”与“方程f(x)=0的根”,以及应用导数研究函数的方法。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2012-2013学年吉林省吉林市高三三模(期末)理科数学试卷(解析版) 题型:选择题
已知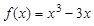 ,并设:
,并设:
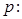
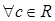 ,
,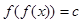 至少有3个实根;
至少有3个实根;
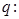 当
当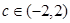 时,方程
时,方程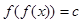 有9个实根;
有9个实根;
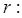 当
当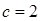 时,方程
时,方程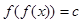 有5个实根。
有5个实根。
则下列命题为真命题的是( )
A.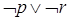 B.
B. 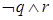 C. 仅有
C. 仅有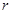 D.
D. 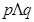
查看答案和解析>>
科目:高中数学 来源:2012-2013学年吉林省吉林市高三三模(期末)文科数学试卷(解析版) 题型:选择题
已知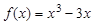 ,并设:
,并设:
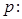
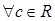 ,
,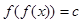 至少有3个实根;
至少有3个实根;
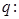 当
当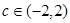 时,方程
时,方程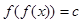 有9个实根;
有9个实根;
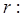 当
当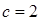 时,方程
时,方程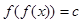 有5个实根.
有5个实根.
则下列命题为真命题的是( )
A.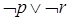 B.
B. 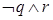 C.
仅有
C.
仅有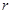 D.
D. 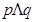
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com