
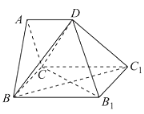
【题目】如图,多面体![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 为原正三棱柱的底面,
为原正三棱柱的底面,![]() ,点D为
,点D为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() ,由题意可得四边形
,由题意可得四边形![]() 是正方形,且
是正方形,且![]() ,再由点D为
,再由点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由线面垂直的判定可得;
,由线面垂直的判定可得;
(2)取BC的中点O,连接AO,可得AO⊥BC,由正棱柱的性质可得AO⊥平面![]() ,以O为坐标原点,向量
,以O为坐标原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面
分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() .
.
∵多面体![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四边形![]() 是正方形,且
是正方形,且![]() .
.
∵点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点O,连接
的中点O,连接![]() .
.
∵![]() 为正三角形,
为正三角形,![]() .
.
由正棱柱的性质可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
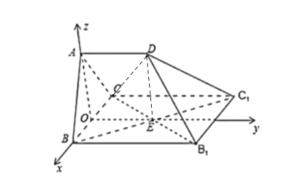
以点O为原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴正方向建立如图所示空间直角坐标系
分别为x、y,z轴正方向建立如图所示空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则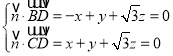 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
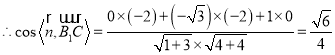 ,
,
又∵二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:
【题目】某地拟建造一座大型体育馆,其设计方案侧面的外轮廓如图所示,曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]() ;曲线
;曲线![]() 是抛物线
是抛物线![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.假定拟建体育馆的高
的半径.假定拟建体育馆的高![]() (单位:米,下同).
(单位:米,下同).
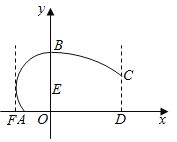
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的长度;
的长度;
(2)若要求体育馆侧面的最大宽度![]() 不超过
不超过![]() 米,求
米,求![]() 的取值范围;
的取值范围;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,![]() =λ
=λ![]() .
.
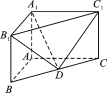
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1- A1C1-D的大小为60°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌奶茶公司计划在A地开设若干个连锁加盟店,经调查研究,加盟店的个数x与平均每个店的月营业额y(万元)具有如下表所示的数据关系:
x | 2 | 4 | 6 | 8 | 10 |
y | 20.9 | 20.2 | 19 | 17.8 | 17.1 |
(1)求y关于x的线性回归方程;
(2)根据(1)中的结果分析,为了保证平均每个加盟店的月营业额不少于14.6万元,则A地开设加盟店的个数不能超过几个?
参考公式:线性回归方程![]() 中的斜率和截距的最小二乘估计公式分别为
中的斜率和截距的最小二乘估计公式分别为
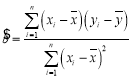 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
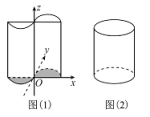
【题目】我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图(1),函数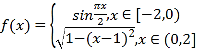 的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
的图象与x轴围成一个封闭区域A(阴影部分),将区域A(阴影部分)沿z轴的正方向上移6个单位,得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示,其底面积与区域A(阴影部分)的面积相等,则此柱体的体积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥
中,BO、AO、CO所在直线两两垂直,且AO=CO,∠BAO=60°,E是AC的中点,三棱锥![]() 的体积为
的体积为![]()
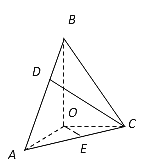
(1)求三棱锥![]() 的高;
的高;
(2)在线段AB上取一点D,当D在什么位置时,![]() 和
和![]() 的夹角大小为
的夹角大小为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数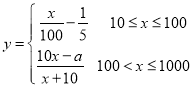 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com