
设有两个命题:
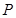 :方程
:方程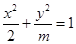 表示焦点在
表示焦点在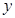 轴上的椭圆;
轴上的椭圆;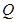 :关于
:关于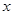 的不等式
的不等式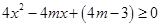 在
在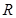 上恒成立;如果这两个命题有且只有一个真命题,则实数
上恒成立;如果这两个命题有且只有一个真命题,则实数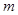 的取值范围是________
的取值范围是________
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 7 |
| 2 |
| 7 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年新课标版高一数学必修一(指数函数与对数函数念)单元测试 题型:解答题
若关于 的方程
的方程 有实根,求
有实根,求 的取值范围。
的取值范围。
变题1:设有两个命题:①关于 的方程
的方程 有解;②函数
有解;②函数 是减函数。当①与②至少有一个真命题时,实数
是减函数。当①与②至少有一个真命题时,实数 的取值范围是__
的取值范围是__
变题2:方程 的两根均大于1,则实数a的取值范围是_____。
的两根均大于1,则实数a的取值范围是_____。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com