
【题目】新能源汽车的春天来了!2018年3月5日上午,李克强总理做政府工作报告时表示,将新能源汽车车辆购置税优惠政策再延长三年,自2018年1月1日至2020年12月31日,对购置的新能源汽车免征车辆购置税.某人计划于2018年5月购买一辆某品牌新能源汽车,他从当地该品牌销售网站了解了近五个月的实际销量如下表:
月份 | 2017.12 | 2018.01 | 2018.02 | 2018.03 | 2018.04 |
月份编号 | 1 | 2 | 3 | 4 | 5 |
销量(万量) | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
(1)经分析,可用线性回归模型拟合当地该品牌新能源汽车实际销量![]() (万辆)与月份编号
(万辆)与月份编号![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量;
,并预测2018年5月份当地该品牌新能源汽车的销量;
(2)2018年6月12日,中央财政和地方财政将根据新能源汽车的最大续航里程(新能源汽车的最大续航里程是指理论上新能源汽车所装的燃料或电池所能够提供给车跑的最远里程)对购车补贴进行新一轮调整.已知某地拟购买新能源汽车的消费群体十分庞大,某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查,得到如下一份频数表:
补贴金额预期值区间(万元) |
|
|
|
|
|
|
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
(i)求这200位拟购买新能源汽车的消费者对补贴金额的心理预期值![]() 的方差
的方差![]() 及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
及中位数的估计值(同一区间的预期值可用该区间的中点值代替,估计值精确到0.1);
(ii)将频率视为概率,现用随机抽样方法从该地区拟购买新能源汽车的所有消费者中随机抽取3人,记被抽取的3人中对补贴金额的心理预期值不低于3万元的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附:①回归直线的斜率和截距的最小二乘估计公式分别为: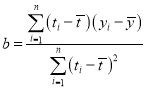 ,
,![]() ;②
;②![]() .
.
【答案】(1) ![]() ,2万辆. (2) (i)
,2万辆. (2) (i)![]() =1.7,中位数3.3万元.(ii)分布列见解析,数学期望为1.8
=1.7,中位数3.3万元.(ii)分布列见解析,数学期望为1.8
【解析】
(1)由题意利用最小二乘法能求出y关于t的线性回归方程![]() ,并预测2018年5月份当地该品牌新能源汽车的销量.
,并预测2018年5月份当地该品牌新能源汽车的销量.
(2)(i)由题意能求出这200位拟购买新能源汽车的消费者对补贴金额的心里预期值![]() 的平均值
的平均值![]() 和样本方差s2及中位数的估计值.
和样本方差s2及中位数的估计值.
(ii)根据给定的频数表可知,任意抽取1名拟购买新能源汽车的消费者,对补贴金额的心理预期值不低于3万元的概率为![]() ,由题意可知ξ~B(3,
,由题意可知ξ~B(3,![]() ),ξ的所有可能取值为0,1,2,3,由此能求出ξ的分布列及数学期望E(ξ).
),ξ的所有可能取值为0,1,2,3,由此能求出ξ的分布列及数学期望E(ξ).
(1)由表格数据可知,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
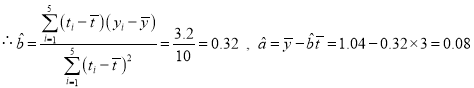 ,
,
![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,
,
根据![]() 的含义,2018年5月时,
的含义,2018年5月时,![]() ,代入可得
,代入可得![]() (万辆),即2018年5月销量的预测值为2万辆.
(万辆),即2018年5月销量的预测值为2万辆.
(2)(i)由表中数据可知各组频率依次为0.1,0.3,0.3,0.15,0.1,0.05,
平均值![]() ,
,
![]()
![]() .
.
![]() ,
,
![]() 中位数在区间
中位数在区间![]() 内,设中位数为
内,设中位数为![]() ,
,
有![]() ,
,
解得,![]() ,
,![]() 中位数
中位数![]() 万元.
万元.
(ii)由(i)可知,心理预期值不低于3万元的概率为![]() ,
,
则![]() ,
,![]() 的可能取值为0,1,2,3.
的可能取值为0,1,2,3.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
| 0.064 | 0.288 | 0.432 | 0.216 |
故![]()


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
【题目】某种植基地将编号分别为1,2,3,4,5,6的六个不同品种的马铃薯种在如图所示的
A | B | C | D | E | F |
这六块实验田上进行对比试验,要求这六块实验田分别种植不同品种的马铃薯,若种植时要求编号1,3,5的三个品种的马铃薯中至少有两个相邻,且2号品种的马铃薯不能种植在A、F这两块实验田上,则不同的种植方法有 ( )
A. 360种 B. 432种 C. 456种 D. 480种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正三角形![]() ,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设
,挖去以三边中点为顶点的小正三角形,得到一个新的图形,这样的过程称为一次“镂空操作“,设![]() 是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设
是一个边长为1的正三角形,第一次“镂空操作”后得到图1,对剩下的3个小正三角形各进行一次“镂空操作”后得到图2,对剩下的小三角形重复进行上述操作,设![]() 是第
是第![]() 次挖去的小三角形面积之和(如
次挖去的小三角形面积之和(如![]() 是第1次挖去的中间小三角形面积,
是第1次挖去的中间小三角形面积,![]() 是第2次挖去的三个小三角形面积之和),
是第2次挖去的三个小三角形面积之和),![]() 是前
是前![]() 次挖去的所有三角形的面积之和,则
次挖去的所有三角形的面积之和,则![]() ( )
( )
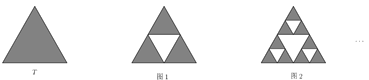
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在线段
分别在线段![]() 、
、![]() 上,且
上,且![]() ,其中
,其中![]() ,连接
,连接![]() ,延长
,延长![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 时,求二面角
时,求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)若直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 值.
值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 的斜率
的斜率![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,
,![]() 轴上是否存在点
轴上是否存在点![]() ,总有
,总有![]() ?若存在,求出点
?若存在,求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系xOy,在x轴的正半轴上,依次取点![]() ,
,![]() ,
,![]() ,
,![]() ,并在第一象限内的抛物线
,并在第一象限内的抛物线![]() 上依次取点
上依次取点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,使得
,使得![]() 都为等边三角形,其中
都为等边三角形,其中![]() 为坐标原点,设第n个三角形的边长为
为坐标原点,设第n个三角形的边长为![]() .
.
⑴求![]() ,
,![]() ,并猜想
,并猜想![]() 不要求证明);
不要求证明);
⑵令![]() ,记
,记![]() 为数列
为数列![]() 中落在区间
中落在区间![]() 内的项的个数,设数列
内的项的个数,设数列![]() 的前m项和为
的前m项和为![]() ,试问是否存在实数
,试问是否存在实数![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的取值范围;若不存在,说明理由;
的取值范围;若不存在,说明理由;
⑶已知数列![]() 满足:
满足:![]() ,数列
,数列![]() 满足:
满足:![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在坐标原点,离心率等于
的中心在坐标原点,离心率等于![]() ,该椭圆的一个长轴端点恰好是抛物线
,该椭圆的一个长轴端点恰好是抛物线![]() 的焦点.
的焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 的两个交点记为
的两个交点记为![]() 、
、![]() ,其中点
,其中点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.当
两侧的动点.当![]() 、
、![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值?若是,求出该定值;若不是,请说明理由.
的斜率是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二十四节气是中国古代的一种指导农事的补充历法,是我国劳动人民长期经验的积累成果和智慧的结晶,被誉为“中国的第五大发明”.由于二十四节气对古时候农事的进行起着非常重要的指导作用,所以劳动人民编写了很多记忆节气的歌谣:春雨惊春清谷天,夏满芒夏暑相连,秋处露秋寒霜降,冬雪雪冬小大寒.《易经》里对二十四节气的晷影长的记录中,冬至和夏至的晷影长是实测得到的,其他节气的晷影是按照等差数列的规律计算出来的,在下表中,冬至的晷影最长为130.0寸,夏至的晷影最短为14.8寸,那么《易经》中所记录的清明的晷影长应为( )

A.77.2寸B.72.4寸C.67.3寸D.62.8寸
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com