
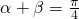 ,则(1+tanα)•(1+tanβ)=________.
,则(1+tanα)•(1+tanβ)=________. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:3年高考2年模拟:4.2 三角函数的图象和性质及三角恒等变换(6)(解析版) 题型:选择题
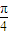 ,
,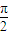 ),则f(sinθ)>f(cosθ);
),则f(sinθ)>f(cosθ);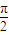 ;
;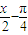 )的图象,只需将y=sin
)的图象,只需将y=sin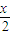 的图象向左平移
的图象向左平移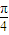 个单位.
个单位.查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省攀枝花七中高三(下)开学数学试卷(理科)(解析版) 题型:填空题
 平移可得曲线(x+1)2-(y-3)2=1;
平移可得曲线(x+1)2-(y-3)2=1; ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线; 与
与 夹角为锐角θ,且满足
夹角为锐角θ,且满足  ,则点P的轨迹是圆(除去与直线AB的交点);
,则点P的轨迹是圆(除去与直线AB的交点);查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市南丰中学高三(上)数学复习试卷C (必修4)(解析版) 题型:选择题
 ,则cosα的值为( )
,则cosα的值为( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com