
【题目】已知f(x)=![]() ,x∈(-2,2).
,x∈(-2,2).
(1) 判断f(x)的奇偶性并说明理由;
(2) 求证:函数f(x)在(-2,2)上是增函数;
(3) 若f(2+a)+f(1-2a)>0,求实数a的取值范围.
【答案】(1) 见解析:(2) 见解析:(3) a∈![]() .
.
【解析】试题分析:(1)定义域 关于原点对称,同时满足f(x)=-f(-2),所以是奇函数。(2)由定义法证明函数的单调性,按假设,作差,变形,判断,下结论过程完成。(3)由奇函数,原不等式变形为f(2+a)>-f(1-2a)=f(2a-1),再由函数单调性及定义域可知![]() ,解不等式组可解。
,解不等式组可解。
试题解析:(1) 解:∵ f(-x)=![]() =-
=-![]() =-f(x),∴ f(x)是奇函数.
=-f(x),∴ f(x)是奇函数.
(2) 证明:设x1,x2为区间(-2,2)上的任意两个值,且x1<x2,则f(x1)-f(x2)=![]() -
-![]()
=![]() ,
,
因为-2<x1<x2<2,所以x2-x1>0,x1x2-4<0,所以f(x1)-f(x2)<0,f(x1)<f(x2),
所以函数f(x)在(-2,2)上是增函数.
(3) 解:因为f(x)为奇函数,所以由f(2+a)+f(1-2a)>0得,f(2+a)>-f(1-2a)=f(2a-1),
因为函数f(x)在(-2,2)上是增函数,
所以![]() 即
即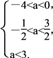
故a∈![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】2016年1月1日起全国统一实施全面两孩政策.为了解适龄民众对放开生育二胎政策的态度,某市选取70后和80后作为调查对象,随机调查了100位,得到数据如表:
生二胎 | 不生二胎 | 合计 | |
70后 | 30 | 15 | 45 |
80后 | 45 | 10 | 55 |
合计 | 75 | 25 | 100 |
(1)以这100个人的样本数据估计该市的总体数据,且以频率估计概率,若从该市70后公民中随机抽取3位,记其中生二胎的人数为X,求随机变量X的分布列和数学期望;
(2)根据调查数据,是否有90%以上的把握认为“生二胎与年龄有关”,并说明理由.
参考数据:
P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥C的底面是正方形,PA⊥平面ABCD,PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PEC
(2)求证:平面PCD⊥平面PEC;
(3)求三棱锥C-BEP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机器人的运动轨道是边长为1米的正三角形ABC,开机后它从A点出发,沿轨道先逆时针运动再顺时针运动,每运动6米改变一次运动方向(假设按此方式无限运动下去),运动过程中随时记录逆时针运动的总路程s1和顺时针运动的总路程s2,x为该机器人的“运动状态参数”,规定:逆时针运动时x=s1,顺时针运动时x=-s2,机器人到A点的距离d与x满足函数关系d=f(x),现有如下结论:
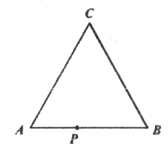
①f(x)的值域为[0,1];
②f(x)是以3为周期的函数;
③f(x)是定义在R上的奇函数;
④f(x)在区间[-3,-2]上单调递增.
其中正确的有_________(写出所有正确结论的编号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(ex+1)(ax+2a﹣2),若存在x∈(0,+∞),使得不等式f(x)﹣2<0成立,则实数a的取值范围是( )
A.(0,1)
B.(0, ![]() )
)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示几何体ABC﹣A1B1C1中,A1、B1、C1在面ABC上的射影分别是线段AB、BC、AC的中点,面A1B1C1∥面ABC,△ABC是边长为2的等边三角形. 
(1)求证:△A1B1C1是等边三角形;
(2)若面ACB1A1⊥面BA1B1 , 求该几何体ABC﹣A1B1C1的体积;
(3)在(2)的条件下,求面ABC与面A1B1B所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设动直线![]() 与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与
与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=x﹣ ![]() sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
sin2x+asinx在(﹣∞,+∞)单调递增,则a的取值范围是( )
A.[﹣1,1]
B.[﹣1, ![]() ]
]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣1,﹣ ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com