分析:(1)先在四边形AA1B1B中,利用一组对边平行且相等证出四边形B1NAM是平行四边形,从而B1N∥AM,再结合直线与平面平行的判定定理,可得直线B1N∥平面AMC1,再用同样的方法证出CN∥平面AMC1,最后利用平面与平面平行的判定定理,可以证出平面AMC1∥平面NB1C;
(2)先根据直三棱柱的性质,利用线面垂直证出C1M⊥BB1,结合等腰三角形A1B1C1中,中线C1M⊥A1B1,利用直线与平面垂直的判定定理,证出C1M⊥平面AA1B1B,从而得到直线C1M⊥A1B,再结合已知条件AC1⊥A1B,得到A1B⊥平面AC1M,结合AM?平面AC1M,最终得到A1B⊥AM.
解答:证明(1)∵M,N分别为A
1B
1,AB中点,

∴B
1M∥NA且B
1M=NA,
∴四边形B
1NAM是平行四边形
∴B
1N∥AM
又∵AM?平面AMC,B
1N?平面AMC
1,
∴B
1N∥平面AMC
1连接MN,
∵矩形BB
1A
1A中,M、N分别是A
1B
1、AB的中点
∴BB
1∥MN且BB
1=MN
∵BB
1∥CC
1且BB
1=CC
1∴四边形CC
1MN是平行四边形,
∴MC
1∥CN,
∵MC
1?平面AMC,CN?平面AMC
1,
∴CN∥平面AMC
1,
∵CN?平面B
1CN,B
1N?平面B
1CN,CN∩B
1N=N,
∴平面B
1CN∥平面AMC
1;
(2)∵三棱柱ABC-A
1B
1C
1是直三棱柱,
BB
1⊥平面A
1B
1C
1,C
1M?平面A
1B
1C
1
∴C
1M⊥BB
1
又∵B
1C
1=A
1C
1,M为A
1B
1中点,
∴C
1M⊥A
1B
1,
∵A
1B
1∩BB
1=B
1,A
1B
1、BB
1?平面AA
1B
1B
∴C
1M⊥平面AA
1B
1B,
∵A
1B?平面AA
1B
1B,
∴C
1M⊥A
1B,
又∵AC
1⊥A
1B,C
1M∩AC
1=C
1,C
1M、AC
1?平面AC
1M,
∴A
1B⊥平面AC
1M,
∵AM?平面AC
1M,
∴A
1B⊥AM.
点评:本题在一个特殊的直三棱柱中,通过证明平面与平面平行和两条异面直线互相垂直,着重考查了面面平行的判定定理和线面垂直的判定与性质,属于中档题.

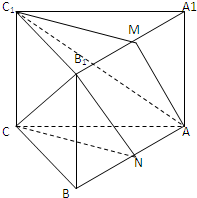 直三棱柱中ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别为A1B1,AB中点,
直三棱柱中ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别为A1B1,AB中点,


 金钥匙试卷系列答案
金钥匙试卷系列答案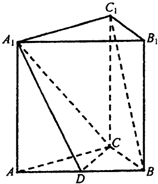 直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC=
直三棱柱A1B1C1-ABC中,AC⊥CB,D为AB中点,CB=1,AC= 如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.
如图,直三棱柱A1B1C1-ABC中,C1C=CB=CA=2,AC⊥CB.D、E分别为棱C1C、B1C1的中点.