
(1)求点D到平面PAC的距离;
(2)若点M分![]() 的比为2∶1,求二面角M-CD-A的大小.
的比为2∶1,求二面角M-CD-A的大小.
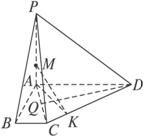
解法一:(1)过D作DQ⊥AC于Q.

∵PA⊥平面ABCD,
∴PA⊥DQ.
∴DQ⊥平面PAC.又由S△ACD=![]() AD·AB=
AD·AB=![]() AC·DQ,
AC·DQ,
AC=![]() ,∴DQ=
,∴DQ=![]() .
.
∴D到平面PAC的距离为![]() .
.
(2)过A作AK⊥DC于K点,连结MK.
∵PA⊥平面ABCD,∴MK⊥CD.
∴∠MKA为M-CD-A的平面角.
∵PA=AD=3,又![]() =2,∴PM=2,MA=1.
=2,∴PM=2,MA=1.
在△ACD中,由面积相等,得AD·AB=CD·AK.
又CD=![]() ,∴AK=
,∴AK=![]() .
.
∴tan∠MKA=![]() =
=![]() ,
,
即二面角的大小为arctan![]() .
.
解法二:以A为坐标原点,以![]() 所在直线为x、y、z轴建立坐标系.
所在直线为x、y、z轴建立坐标系.
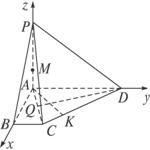
(1)过D作DQ⊥AC于Q,
∵PA⊥DQ,
∴DQ⊥平面PAC.
∴DQ就是D到平面PAC的距离.
设![]() =m
=m![]() =m(
=m(![]() )=m(2,1,0),
)=m(2,1,0),
∴![]() =(0,-3,0)+m(2,1,0)=(2m,m-3,0).
=(0,-3,0)+m(2,1,0)=(2m,m-3,0).
由![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =4m2+m(m-3)=0.
=4m2+m(m-3)=0.
∴m=![]() .
.
|![]() |=
|=![]() =
=![]() .
.
(2)过A作AK⊥DC于K,设![]() = λ
= λ![]() =λ(2,-2,0).
=λ(2,-2,0).
则![]() =(2λ,3-2λ,0).
=(2λ,3-2λ,0).
∵![]() ⊥
⊥![]() ,∴
,∴![]() ·
·![]() =0.∴λ=34.
=0.∴λ=34.
∴|![]() |=
|=![]() .
.
∵MA⊥平面ABCD,∴MK⊥CD.
∴∠MKA就是M-CD-A的平面角.
∴tan∠MKA=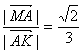 .
.
∴∠MKA=arctan![]() .
.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源:黄冈中学 高一数学(下册)、第五章 平面向量单元(5.1~5.5)测试卷 题型:044
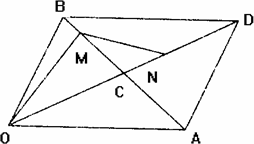
如图所示,已知四边形OADB是以向量![]() ,
,![]() 为边的平行四边形,其中
为边的平行四边形,其中![]() ,
,![]() .试以向量a,b为一组基底,表示出向量
.试以向量a,b为一组基底,表示出向量![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)异面直线PM与FQ所成的角;
(2)四面体P-EFB的体积;
(3)异面直线PM与FQ的距离.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
如图所示,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点。

(Ⅰ)求证:平面FGH⊥平面AEB;
(Ⅱ)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com