
已知定圆 ,动圆
,动圆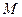 过点
过点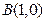 且与圆
且与圆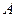 相切,记动圆圆
相切,记动圆圆
心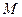 的轨迹为
的轨迹为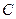 .
.
(Ⅰ)求曲线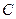 的方程;
的方程;
(Ⅱ)若点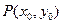 为曲线
为曲线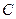 上任意一点,证明直线
上任意一点,证明直线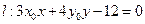 与曲线
与曲线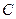 恒有且只有一个公共点.
恒有且只有一个公共点.
(Ⅲ)由(Ⅱ)你能否得到一个更一般的结论?并且对双曲线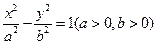 写出一个类似的结论(皆不必证明).
写出一个类似的结论(皆不必证明).
解:(Ⅰ)由题知圆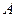 圆心为
圆心为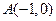 ,半径为
,半径为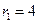 ,设动圆
,设动圆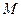 的圆心为
的圆心为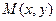
半径为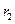 ,
,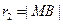 ,由
,由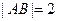 ,可知点
,可知点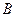 在圆
在圆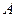 内,所以点
内,所以点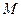 的轨迹是以
的轨迹是以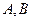 为焦点
为焦点
的椭圆,设椭圆的方程为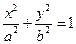
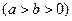 ,由
,由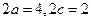 ,得
,得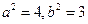 ,
,
故曲线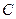 的方程为
的方程为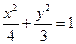 ………………………………4分
………………………………4分
(Ⅱ)当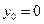 时,由
时,由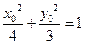 可得
可得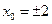
当 ,
,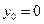 时,直线
时,直线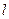 的方程为
的方程为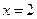 ,直线
,直线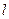 与曲线
与曲线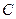 有且只有一个交点
有且只有一个交点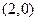
当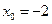 ,
,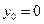 时,直线
时,直线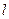 的方程为
的方程为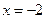 ,直线
,直线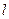 与曲线
与曲线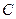 有且只有一个交点
有且只有一个交点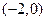
当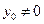 时得
时得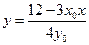 ,代入
,代入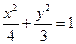 ,消去
,消去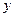 整理得:
整理得: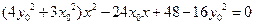 --------------------------------① …………6分
--------------------------------① …………6分
由点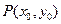 为曲线
为曲线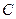 上一点,故
上一点,故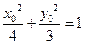 .即
.即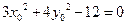
于是方程①可以化简为: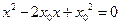
解得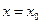 .将
.将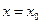 代入
代入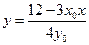 得
得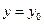 ,说明直线与曲线有且只有一个交点
,说明直线与曲线有且只有一个交点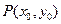 .
.
综上,不论点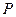 在何位置,直线
在何位置,直线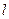 :
: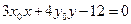 与曲线
与曲线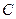 恒有且只有一个交点,交点即
恒有且只有一个交点,交点即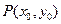 …………………………………………8分
…………………………………………8分
(Ⅲ)更一般的结论:对椭圆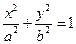
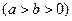 ,过其上任意一点
,过其上任意一点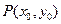 的切线方程为
的切线方程为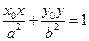 ;
;
在双曲线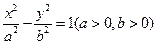 中的类似的结论是:过双曲线
中的类似的结论是:过双曲线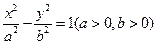 上任意一点
上任意一点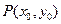 的切线方程为:
的切线方程为: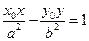 .…………………………………12分
.…………………………………12分
解析


科目:高中数学 来源: 题型:
(03年北京卷理)(13分)
已知动圆过定点P(1,0),且与定直线![]() 相切,点C在l上.
相切,点C在l上.
(Ⅰ)求动圆圆心的轨迹M的方程;
(Ⅱ)设过点P,且斜率为-![]() 的直线与曲线M相交于A,B两点.
的直线与曲线M相交于A,B两点.
(i)问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由;
(ii)当△ABC为钝角三角形时,求这种点C的纵坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011届贵州省五校高三第五次联考文科数学(暨遵义四中第13次月考) 题型:解答题
已知定圆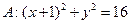 ,动圆
,动圆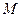 过点
过点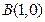 且与圆
且与圆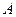 相切,记动圆圆
相切,记动圆圆
心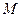 的轨迹为
的轨迹为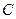 .
.
(Ⅰ)求曲线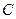 的方程;
的方程;
(Ⅱ)若点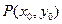 为曲线
为曲线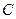 上任意一点,证明直线
上任意一点,证明直线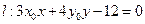 与曲线
与曲线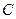 恒有且只有一个公共点.
恒有且只有一个公共点.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省第13次月考) 题型:解答题
已知定圆 ,动圆
,动圆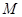 过点
过点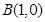 且与圆
且与圆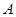 相切,记动圆圆
相切,记动圆圆
心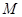 的轨迹为
的轨迹为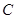 .
.
(Ⅰ)求曲线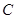 的方程;
的方程;
(Ⅱ)若点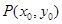 为曲线
为曲线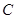 上任意一点,证明直线
上任意一点,证明直线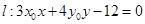 与曲线
与曲线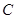 恒有且只有一个公共点.
恒有且只有一个公共点.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年贵州省第五校高三第五次联考理科数学(暨遵义四中13次月考) 题型:解答题
已知定圆 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆
心 的轨迹为
的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若点 为曲线
为曲线 上任意一点,证明直线
上任意一点,证明直线 与曲线
与曲线 恒有且只有一个公共点.
恒有且只有一个公共点.
(Ⅲ)由(Ⅱ)你能否得到一个更一般的结论?并且对双曲线 写出一个类似的结论(皆不必证明).
写出一个类似的结论(皆不必证明).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com