
【题目】已知集合![]()
(1)若![]() ,求
,求![]() 的取值范围.
的取值范围.
(2)若![]() ,且
,且![]() (
(![]() 为整数集合),求
为整数集合),求![]() 的取值范围.
的取值范围.
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C的离心率为![]() ,且椭圆C过点
,且椭圆C过点![]() .
.
(1)求椭圆C的标准方程:
(2)若直线l:![]() 与椭圆C相交于A,B两点(A,B不是左右顶点),且以
与椭圆C相交于A,B两点(A,B不是左右顶点),且以![]() 为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在圆心角为直角,半径为![]() 的扇形区域内进行野外生存训练.如图所示,在相距
的扇形区域内进行野外生存训练.如图所示,在相距![]() 的
的![]() ,
,![]() 两个位置分别为300,100名学生,在道路
两个位置分别为300,100名学生,在道路![]() 上设置集合地点
上设置集合地点![]() ,要求所有学生沿最短路径到
,要求所有学生沿最短路径到![]() 点集合,记所有学生进行的总路程为
点集合,记所有学生进行的总路程为![]() .
.
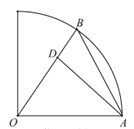
(1)设![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)当![]() 最小时,集合地点
最小时,集合地点![]() 离点
离点![]() 多远?
多远?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A. 回归直线一定过样本中心![]()
B. 残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C. 两个模型中残差平方和越小的模型拟合的效果越好
D. 甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人2013-2017这五年的年度体检的血压值的折线图如图所示.

(1)根据散点图,直接判断甲、乙这五年年度体检的血压值谁的波动更大,并求波动更大者的方差;
(2)根据乙这五年年度体检血压值的数据,求年度体检血压值![]() 关于年份
关于年份![]() 的线性回归方程,并据此估计乙在2018年年度体检的血压值.
的线性回归方程,并据此估计乙在2018年年度体检的血压值.
(附: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某镇有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() ,
,![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.

(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com