已知函数F(x)=m•3x+n•2x(m,n均为非零常数).
(1)若m+n=0,解关于x的方程F(x)=0;
(2)求证:当m<0,n<0时,F(x)为R上的单调减函数;
(3)若mn<0,求满足F(x+1)≤F(x)的x的取值范围.
解:(1)∵函数F(x)=m•3
x+n•2
x(m,n均为非零常数),m+n=0,即n=-m,
∴函数F(x)=m•3
x-m•2
x =m( 3
x-2
x ),故方程F(x)=0即 m( 3
x-2
x )=0,
故有 3
x-2
x=0,∴x=0.
(2)证明:当m<0,n<0时,设x
1<x
2,
∵F(x
1)-F(x
2)=m
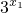
+n

-(m
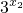
+n

)=m(
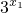
-
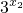
)+n(

-

),
由指数函数的单调性可得
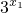
-
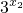
<0,

-

<0.
∴m(
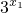
-
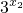
)>0,n(

-

)>0,∴F(x
1)-F(x
2)>0,故 F(x
1)>F(x
2),
故F(x)为R上的单调减函数.
(3)不等式F(x+1)≤F(x)即m3
x+1+n2
x+1≤(m•3
x+n•2
x),
即m(3
x+1-3
x)≤n(2
x-2
x+1)=-n(2
x+1-2
x),即2m3
x≤-n 2
x .
当 m>0、n<0时,不等式可化为
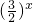
≤-
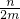
,解得 x≤
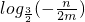
.
当m<0、n>0时,不等式可化为
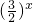
≥-
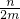
,解得 x≥
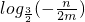
.
分析:(1)由题意可得函数F(x)=m( 3
x-2
x ),故方程F(x)=0即 m( 3
x-2
x )=0,故有 3
x-2
x=0,解得x=0.
(2)当m<0,n<0时,设x
1<x
2,化简F(x
1)-F(x
2)=m(
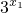
-
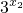
)+n(

-

)>0,从而可得F(x)为R上的单调减函数.
(3)不等式可化为m3
x+1+n2
x+1≤(m•3
x+n•2
x),即2m3
x≤-n 2
x .分 m>0、n<0和m<0、n>0两种情况,分别利用不等式的性质,求出不等式的解集.
点评:本题主要考查指数型函数的性质以及应用,体现了分类讨论的数学思想,属于中档题.

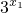 +n
+n -(m
-(m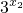 +n
+n )=m(
)=m(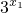 -
-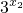 )+n(
)+n( -
- ),
),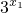 -
-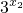 <0,
<0, -
- <0.
<0.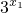 -
-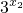 )>0,n(
)>0,n( -
- )>0,∴F(x1)-F(x2)>0,故 F(x1)>F(x2),
)>0,∴F(x1)-F(x2)>0,故 F(x1)>F(x2),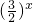 ≤-
≤-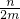 ,解得 x≤
,解得 x≤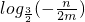 .
.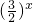 ≥-
≥-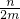 ,解得 x≥
,解得 x≥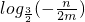 .
.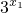 -
-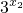 )+n(
)+n( -
- )>0,从而可得F(x)为R上的单调减函数.
)>0,从而可得F(x)为R上的单调减函数.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案