练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若点P在△AOB的边AB上，且数学公式=m数学公式+4n数学公式（m，n∈R），则mn的最大值为________．


    分析：求出 和 ，由 ∥，可得 m+4n=1，利用基本不等式可得 mn≤，从而得到答案．
    解答：∵=-=（m-1）+4n，=-=-m+（1-4n），
    由于点P在△AOB的边AB上，故m、n 都是正数，且 ∥，∴（m-1）（1-4n）-4n（-m）=0，
    化简可得 m+4n=1，由基本不等式可得 1≥2，∴mn≤，当且仅当 m=4n=时，
    等号成立，故mn的最大值为 ，
    故答案为：．
    点评：本题考查两个向量共线的性质，两个向量坐标形式的运算，基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    △OAB中，
    OA
    =
    a
    ，
    OB
    =
    b
    ，
    OP
    =
    p
    ，若
    p
    =t(
    a
    |
    a
    |
    +
    b
    |
    b
    |
    )    ，t∈R，则点P一定在（　　）
    A、∠AOB平分线所在直线上
    B、线段AB中垂线上
    C、AB边所在直线上
    D、AB边的中线上

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若点P在△AOB的边AB上，且
    OP
    =m
    OA
    +4n
    OB
    （m，n∈R），则mn的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中,=a,=b,P是△ABC所在平面上一点,记=p.若p=t(),t∈R,则点P在(    )

    A.边AB的垂直平分线上

    B.边AB的中线上

    C.∠AOB的平分线所在直线上

    D.边AB的中线所在直线上

    查看答案和解析>>

    科目：高中数学 来源：2011年广西桂林市、河池市、防城港市高三第一次联考数学试卷（理科）（解析版） 题型：解答题

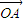    若点P在△AOB的边AB上，且=m+4n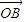（m，n∈R），则mn的最大值为    ．

    查看答案和解析>>

    同步练习册答案