
【题目】已知函数f(x)=ln(1+x)﹣x+ ![]() x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
x2(k≥0). (Ⅰ)当k=2时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)求f(x)的单调区间.
【答案】解:(I)当K=2时, ![]() 由于
由于 ![]() 所以曲线y=f(x)在点(1,f(1))处的切线方程为
所以曲线y=f(x)在点(1,f(1))处的切线方程为![]() .即3x﹣2y+2ln2﹣3=0
.即3x﹣2y+2ln2﹣3=0
(II)f'(x)= ![]() ﹣1+kx(x>﹣1)
﹣1+kx(x>﹣1)
当k=0时, ![]()
因此在区间(﹣1,0)上,f'(x)>0;在区间(0,+∞)上,f'(x)<0;
所以f(x)的单调递增区间为(﹣1,0),单调递减区间为(0,+∞);
当0<k<1时, ![]() ,得
,得 ![]() ;
;
因此,在区间(﹣1,0)和 ![]() 上,f'(x)>0;在区间
上,f'(x)>0;在区间 ![]() 上,f'(x)<0;
上,f'(x)<0;
即函数f(x)的单调递增区间为(﹣1,0)和 ![]() ,单调递减区间为(0,
,单调递减区间为(0, ![]() );
);
当k=1时, ![]() .f(x)的递增区间为(﹣1,+∞)
.f(x)的递增区间为(﹣1,+∞)
当k>1时,由 ![]() ,得
,得 ![]() ;
;
因此,在区间 ![]() 和(0,+∞)上,f'(x)>0,在区间
和(0,+∞)上,f'(x)>0,在区间 ![]() 上,f'(x)<0;
上,f'(x)<0;
即函数f(x)的单调递增区间为 ![]() 和(0,+∞),单调递减区间为
和(0,+∞),单调递减区间为 ![]()
【解析】(I)根据导数的几何意义求出函数f(x)在x=1处的导数,从而求出切线的斜率,然后求出切点坐标,再用点斜式写出直线方程,最后化简成一般式即可;(II)先求出导函数f'(x),讨论k=0,0<k<1,k=1,k>1四种情形,在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0即可.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】对于二次函数y=﹣4x2+8x﹣3,
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)求函数的最大值或最小值;
(3)写出函数的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数y=f(2x﹣1)的定义域是( )
A.{x|0≤x≤1}
B.{x|0≤x≤2}
C.{x| ![]() ≤x≤
≤x≤ ![]() }
}
D.{x|﹣1≤x≤3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=aex﹣x﹣1,a∈R. (Ⅰ)当a=1时,求f(x)的单调区间;
(Ⅱ)当x∈(0,+∞)时,f(x)>0恒成立,求a的取值范围;
(Ⅲ)求证:当x∈(0,+∞)时,ln ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1的参数方程为 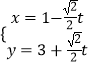 (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2 ![]() sin(θ+
sin(θ+ ![]() ). (Ⅰ)求曲线C1与曲线C2的普通方程;
). (Ⅰ)求曲线C1与曲线C2的普通方程;
(Ⅱ)若点P的坐标为(﹣1,3),且曲线C1与曲线C2交于B,D两点,求|PB||PD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】形如y= ![]() (c>0,b>0)的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数f(x)=loga(x2+x+1)(a>0,a≠1)有最小值,则当c,b的值分别为方程x2+y2﹣2x﹣2y+2=0中的x,y时的“囧函数”与函数y=loga|x|的图象交点个数为( )
(c>0,b>0)的函数因其图象类似于汉字中的“囧”字,故我们把其生动地称为“囧函数”.若函数f(x)=loga(x2+x+1)(a>0,a≠1)有最小值,则当c,b的值分别为方程x2+y2﹣2x﹣2y+2=0中的x,y时的“囧函数”与函数y=loga|x|的图象交点个数为( )
A.1
B.2
C.4
D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆E: ![]() =1(a>b>0)经过点A(0,﹣1),且离心率为
=1(a>b>0)经过点A(0,﹣1),且离心率为 ![]() . (I)求椭圆E的方程;
. (I)求椭圆E的方程;
(II)经过点(1,1),且斜率为k的直线与椭圆E交于不同两点P,Q(均异于点A),问直线AP与AQ的斜率之和是否为定值,若是,求出这个定值;若不是,请说明理由.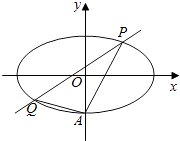
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等轴双曲线C的中心在原点,焦点在x轴上,双曲线C与抛物线y2=16x的准线交于A,B两点,|AB|=4 ![]() ,则双曲线C的实轴长为( )
,则双曲线C的实轴长为( )
A.![]()
B.2 ![]()
C.4
D.4 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,且anan+1+an+1﹣2an=0(n∈N+).
(1)求a2、a3、a4的值;
(2)猜想数列{an}的通项公式,并用数学归纳法加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com