
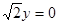 ,经过椭圆
,经过椭圆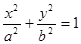 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为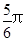 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.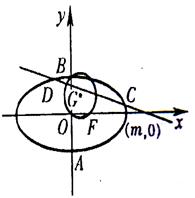
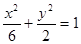 ;(Ⅱ)实数m的取值范围为(
;(Ⅱ)实数m的取值范围为( ,3)。
,3)。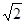 )
)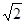 ∴a2=b2+o2=6
∴a2=b2+o2=6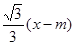 (m>
(m> )
)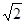 )
)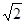 ∴a2=b2+o2=6
∴a2=b2+o2=6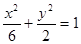 …………………………4分
…………………………4分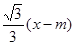 (m>
(m> )
)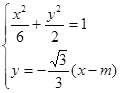
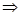 2x2-2mx+(m2-6)=0
2x2-2mx+(m2-6)=0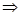 m2<12
m2<12 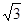 <m<2
<m<2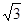 ………………………………………6分
………………………………………6分 ∴
∴ <m<2
<m<2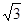 ……………………………………7分
……………………………………7分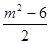
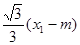 ][-
][-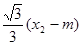 ]=
]=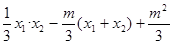
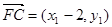
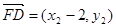
 =(x1-2)(x2-2)+y1y2
=(x1-2)(x2-2)+y1y2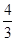 x1x2-
x1x2-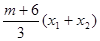 +
+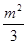 +4
+4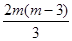 ……………………………………10分
……………………………………10分 <0
<0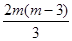 <0
<0 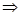 0<m<3
0<m<3 <m<2
<m<2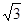
 ,3)………………………………13分
,3)………………………………13分

科目:高中数学 来源:不详 题型:解答题
 的顶点在坐标原点,准线
的顶点在坐标原点,准线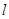 的方程为
的方程为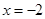 ,点
,点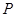 在准线
在准线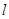 上,纵坐标为
上,纵坐标为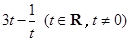 ,点
,点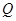 在
在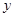 轴上,纵坐标为
轴上,纵坐标为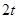 .
.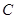 的方程;
的方程;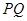 恒与一个圆心在
恒与一个圆心在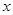 轴上的定圆
轴上的定圆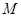 相切,并求出圆
相切,并求出圆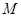 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
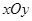 中,圆
中,圆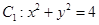 ,圆
,圆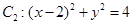 。
。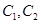 的极坐标方程,并求出圆
的极坐标方程,并求出圆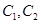 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);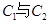 的公共弦的参数方程。
的公共弦的参数方程。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com