
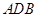 为半圆,
为半圆,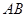 为半圆直径,
为半圆直径,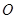 为半圆圆心,且
为半圆圆心,且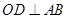 ,
,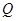 为线段
为线段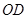 的中点,已知
的中点,已知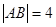 ,曲线
,曲线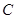 过
过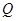 点,动点
点,动点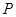 在曲线
在曲线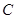 上运动且保持
上运动且保持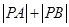 的值不变.
的值不变.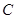 的方程;
的方程;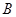 的直线
的直线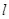 与曲线
与曲线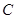 交于
交于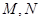 两点,与
两点,与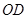 所在直线交于
所在直线交于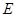 点,
点,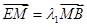 ,
,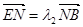 证明:
证明: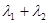 为定值.
为定值.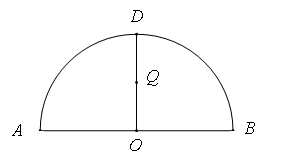
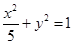 ;(2)
;(2)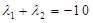 .
.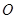 为坐标原点,因为
为坐标原点,因为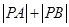 的值不变,所以会想到椭圆的定义,根据椭圆的定义,需要知道
的值不变,所以会想到椭圆的定义,根据椭圆的定义,需要知道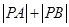 的值,易知
的值,易知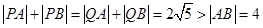 ,故椭圆的基本量就能很快求出,从而求出最终椭圆的标准方程.(2)圆锥曲线与向量的综合,最好使用点的坐标表示,可以根据题意设出
,故椭圆的基本量就能很快求出,从而求出最终椭圆的标准方程.(2)圆锥曲线与向量的综合,最好使用点的坐标表示,可以根据题意设出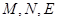 的坐标,利用
的坐标,利用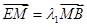 ,
,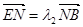 的关系,反求出
的关系,反求出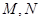 (含
(含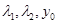 )的坐标代入到椭圆方程中,得到
)的坐标代入到椭圆方程中,得到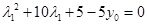 ,
,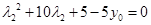 ,可见
,可见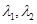 是方程
是方程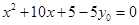 的两个根,故
的两个根,故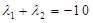 .还可以利用联立方程组的方法,但稍微复杂一点,具体过程见解答.
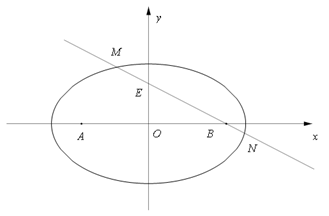
.还可以利用联立方程组的方法,但稍微复杂一点,具体过程见解答.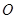 为原点,
为原点,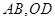 所在直线分别为
所在直线分别为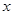 轴,
轴,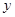 轴,建立平面直角坐标系.
轴,建立平面直角坐标系.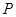 在曲线
在曲线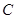 上运动且保持
上运动且保持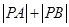 的值不变,而
的值不变,而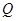 点也在曲线
点也在曲线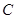 上,
上,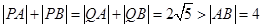 ,满足椭圆的定义,
,满足椭圆的定义,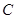 是以原点
是以原点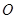 为中心,
为中心,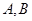 为焦点的椭圆.
为焦点的椭圆. ,
,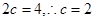 ,
,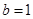
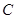 的标准方程为
的标准方程为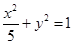
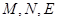 的坐标分别为
的坐标分别为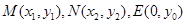 ,则
,则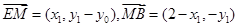
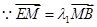 ,
,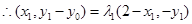
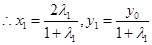 带入到
带入到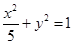 得
得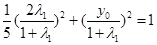
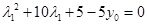
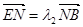 ,得
,得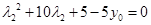
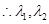 是方程
是方程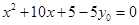 的两个根
的两个根
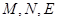 点的坐标分别为
点的坐标分别为 ,
,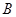 点的坐标为
点的坐标为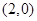 .且点B在椭圆C内,故过点B的直线l必与椭圆C相交.
.且点B在椭圆C内,故过点B的直线l必与椭圆C相交.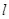 的斜率存在,设直线
的斜率存在,设直线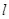 的斜率为
的斜率为 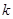 ,则直线
,则直线 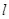 的方程是
的方程是 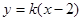
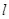 的方程代入到椭圆
的方程代入到椭圆 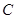 的方程中,消去
的方程中,消去 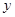 并整理得
并整理得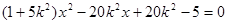 .
.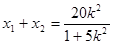 ,
,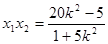
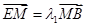 , 则
, 则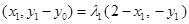 .∴
.∴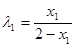 ,
,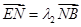 ,∴
,∴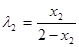
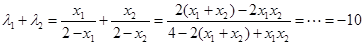 .
.

科目:高中数学 来源:不详 题型:解答题
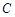 在
在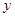 轴右边,
轴右边,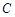 上每一点到点
上每一点到点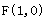 的距离减去它到
的距离减去它到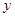 轴距离的差都等于1.
轴距离的差都等于1.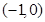 的直线
的直线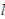 与曲线C有两个交点
与曲线C有两个交点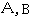 ,且
,且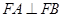 ,求直线
,求直线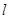 的斜率.
的斜率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
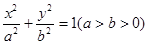 的离心率为
的离心率为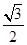 ,
,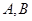 是其左右顶点,
是其左右顶点,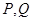 是椭圆上位于
是椭圆上位于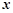 轴两侧的点(点
轴两侧的点(点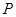 在
在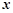 轴上方),且四边形
轴上方),且四边形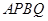 面积的最大值为4.
面积的最大值为4.
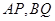 的斜率分别为
的斜率分别为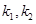 ,若
,若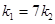 ,设△
,设△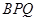 与△
与△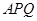 的面积分别为
的面积分别为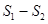 ,求
,求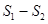 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
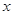 轴上,一个顶点为
轴上,一个顶点为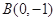 ,且其右焦点到直线
,且其右焦点到直线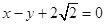 的距离为3.
的距离为3.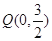 ,与椭圆交于两个不同的点
,与椭圆交于两个不同的点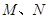 ,且满足
,且满足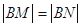 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com