
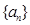 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列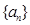 的一个子列.
的一个子列.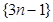 的一个是等比数列的子列;
的一个是等比数列的子列;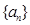 是无穷等比数列,首项
是无穷等比数列,首项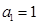 ,公比
,公比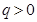 且
且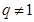 ,则数列
,则数列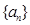 是否存在一个子列
是否存在一个子列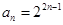 ;(2)证明过程详见解析.
;(2)证明过程详见解析.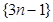 的所有项中任意抽取几项,令其构成等比数列即可,但是至少抽取3项;第二问,分2种情况进行讨论:
的所有项中任意抽取几项,令其构成等比数列即可,但是至少抽取3项;第二问,分2种情况进行讨论: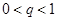 和
和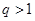 ,利用数列的单调性,先假设存在,在推导过程中找出矛盾即可.
,利用数列的单调性,先假设存在,在推导过程中找出矛盾即可.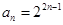 (若只写出2,8,32三项也给满分). 4分
(若只写出2,8,32三项也给满分). 4分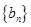 ,通项公式为
,通项公式为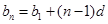 .因为
.因为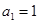
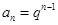 .
.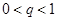 时,
时,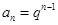 ∈(0,1],且数列
∈(0,1],且数列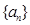 是递减数列,
是递减数列,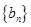 也为递减数列且
也为递减数列且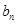 ∈(0,1],
∈(0,1], ,
,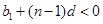 ,得
,得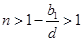 ,
,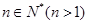 使得
使得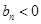 ,这与
,这与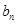 ∈(0,1]矛盾.
∈(0,1]矛盾.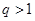 时,
时,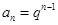 ≥1,数列
≥1,数列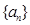 是递增数数列,
是递增数数列,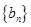 也为递增数列且
也为递增数列且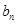 ≥1,
≥1,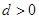 .
.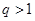 ,
,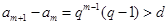 .
.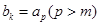 ,则
,则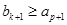 ,
,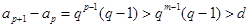 =
=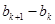 ,
,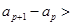
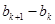 ,即
,即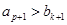 ,但这与
,但这与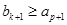 矛盾,说明假设不成立.
矛盾,说明假设不成立.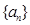 不存在是无穷等差数列的子列. 13分
不存在是无穷等差数列的子列. 13分

 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com