
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)在(1)的条件下,求证:![]() ;
;
(3)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)![]() (2)见解析(3)最大值为
(2)见解析(3)最大值为![]() .
.
【解析】分析:(1)求出导数,写出切线方程![]() ;
;
(2)利用导数求出![]() 的最小值,由最小值>0得结论;
的最小值,由最小值>0得结论;
(3)求出导函数![]() ,其零点为
,其零点为![]() ,首先比较
,首先比较![]() 与
与![]() 的大小,得出
的大小,得出![]() 的单调性,然后再比较
的单调性,然后再比较![]() 大小得出最大值.
大小得出最大值.
详解:(1)当![]() 时,
时,![]() ,所以
,所以![]() ,
,
切线方程为![]() .
.
(2)由(1)知![]() ,则
,则![]() ,当时
,当时![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,函数最小值是
时,函数最小值是![]() ,因此
,因此![]() .
.
(3)![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,设
时,设![]() ,
,
因为![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
且![]() ,所以
,所以![]() 在
在![]() 恒成立,即
恒成立,即![]() ,
,
当![]() ,当
,当![]() ;所以
;所以![]() 在
在![]() 上单调递减,
上单调递减,
在![]() 上单调递增.所以
上单调递增.所以![]() 在
在![]() 上的最大值等于
上的最大值等于![]() ,
,
因为![]() ,
,
设![]() ,所以
,所以![]() .
.
由(2)![]() 在
在![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增.
上单调递增.
又因为![]() ,所以
,所以![]() 在
在![]() 恒成立,即
恒成立,即![]() ,
,
因此当![]() 时,
时,![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),0<β<α<π.
=(cosβ,sinβ),0<β<α<π.
(1)若| ![]() ﹣
﹣ ![]() |=
|= ![]() ,求证:
,求证: ![]() ⊥
⊥ ![]() ;
;
(2)设 ![]() =(0,1),若
=(0,1),若 ![]() +
+ ![]() =
= ![]() ,求α,β的值.
,求α,β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F1 , F2是双曲线C: ![]() (a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的离心率为 .
(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2的最小内角为30°,则C的离心率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知点A(5,-2),B(7,3),且边AC的中点M在y轴上,边BC的中点N在x轴上,求:
(1)顶点C的坐标;
(2)直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )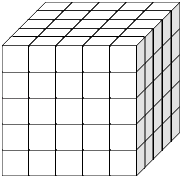
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊毕达哥拉斯学派的数学家研究过各种多边形数,如三角形数1,3,6,10,…,第n个三角形数为 ![]() .记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
.记第n个k边形数为N(n,k)(k≥3),以下列出了部分k边形数中第n个数的表达式:
三角形数 ![]() ,
,
正方形数N(n,4)=n2 ,
五边形数 ![]() ,
,
六边形数N(n,6)=2n2﹣n,
…
可以推测N(n,k)的表达式,由此计算N(10,24)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}满足a1=2,an+1-an=3·22n-1.
(1)求数列{an}的通项公式;
(2)令bn=nan,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数 ![]() 的图象上.
的图象上.
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)已知数列![]() 满足
满足![]() ,若对任意
,若对任意![]() ,存在
,存在![]() 使得
使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com