
四棱锥P-ABCD的底面是边长为a的正方形,PB垂直面ABCD,证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°
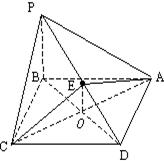
注意到题目中所给的二面角,面PAD与面PCD的棱为PD,围绕PD而考虑问题解决途径.
证法一:利用定义法
经A在PDA平面内作AE⊥PD于E,连CE.
因底是正方形,故CD=DA.
△CED≌△AED,AE=EC,∠CED=∠AED=90°,
则CE⊥PD.
故∠CEA是面PAD与面PCD所成二面角的平面角.
设AC与BD交于O,连EO,则EO⊥AC.
因![]() OA=
OA=![]() ×
×![]() =a,AE<AD<a.
=a,AE<AD<a.
cos∠AEC=![]() =
=![]() <0.
<0.
所以面PAD与面PCD所成的二面角恒大于90°.
证法二:运用三垂线法
∵ PB⊥面ABCD,则PB⊥AD,又AD⊥AB,
∴ AD⊥面PAB,即面PAB⊥面PAD.
过B作BE⊥PA,则BE⊥面PAD.
在面PBC内作PG![]() BC,连GD.
BC,连GD.
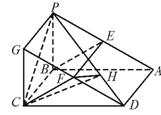
经C作CF⊥面PAD于F,
那么连结EF,有EF![]() AD.
AD.
经F作FH⊥PD于H,连CH,
则∠FHC是所求二面角平面角的补角.
因CF⊥FH,故∠FHC是锐角.
则面PAD与面PCD所成二面角大于90°.
此结论证明过程中与棱锥高无关.
证法三:利用垂面法找平面角.
在证法一所给图形中
连AC、BD,因AC⊥BD,PB⊥面ABCD,
∴ AC⊥PD.
经A作AE⊥PD于E,那么有PD⊥面AEC,连CE,
即PD⊥CE.
故PD与平面AEC垂直后,面AEC与面ADC及面ADP的交线EA、EC构成角∠CEA就是二面角的平面角.
以下同证法一.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
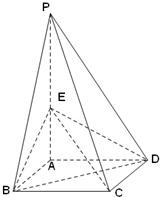 如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.
如图,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PA⊥底面ABCD,且PA=2,E是PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
如图所示,四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,侧面PBC内有BE⊥PC于E,且BE=
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com