Question

【题目】如图，已知四棱锥中，底面为菱形，且， 是边长为的正三角形，且平面平面，点是的中点.

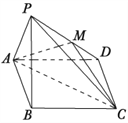
（1）证明： 平面；

（2）求三棱锥的体积.

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）连结交于，连结，由中位线定理可得，根据线面平行的判定定理可得平面；（2）取中点，连结，则平面，由，即可求出三棱锥的体积.

试题解析：（Ⅰ）连结交于，连结，

因为为菱形， ，所以，

由直线不在平面内， 平面，

所以平面.

（Ⅱ）取的中点，连接，则，且.

因为平面平面，所以平面.

所以，

又是中点，所以.

所以 .

【方法点晴】本题主要考查线面平行的判定定理、面面垂直的性质、线面垂直的判定、利用等积变换求三棱锥体积，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面. 本题（1）是就是利用方法①证明的.