
【题目】已知抛物线E:![]() 过点
过点![]() ,过抛物线E上一点
,过抛物线E上一点![]() 作两直线PM,PN与圆C:
作两直线PM,PN与圆C:![]() 相切,且分别交抛物线E于M、N两点.
相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为![]() ,求点P的坐标.
,求点P的坐标.
【答案】(1)抛物线E的方程为![]() ,焦点坐标为
,焦点坐标为![]() ,准线方程为
,准线方程为![]() ;(2)
;(2)![]() 或
或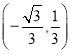
【解析】
(1)将点![]() 代入抛物线方程,可求出抛物线E的方程,进而可求出焦点坐标及准线方程;
代入抛物线方程,可求出抛物线E的方程,进而可求出焦点坐标及准线方程;
(2)设![]() ,
,![]() ,可表示出直线
,可表示出直线![]() 及
及![]() 的斜率的表达式,进而可表示出两直线的方程,再结合直线和圆相切,利用点到直线的距离等于半径,可得
的斜率的表达式,进而可表示出两直线的方程,再结合直线和圆相切,利用点到直线的距离等于半径,可得![]() ,
,![]() 满足方程
满足方程![]() ,从而得到
,从而得到![]() ,又直线MN的斜率为
,又直线MN的斜率为![]() ,可求出
,可求出![]() 的值,即可求出点P的坐标.
的值,即可求出点P的坐标.
(1)将点![]() 代入抛物线方程得,
代入抛物线方程得,![]() ,所以抛物线E的方程为
,所以抛物线E的方程为![]() ,焦点坐标为:
,焦点坐标为:![]() ,准线方程为:
,准线方程为:![]() .
.
(2)由题意知,![]() ,设
,设![]() ,
,![]() ,
,
则直线![]() 的斜率为
的斜率为![]() ,同理,直线PN的斜率为
,同理,直线PN的斜率为![]() ,
,
直线MN的斜率为![]() ,故
,故![]() ,
,
于是直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由直线和圆相切,得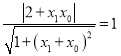 ,
,
即![]() ,
,
同理,直线PN的方程为![]() ,
,
可得![]() ,
,
故![]() ,
,![]() 是方程
是方程![]() 的两根.
的两根.
故![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() 或
或![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
故点P的坐标为![]() 或
或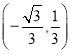 .
.



 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,过左焦点
,过左焦点![]() 的直线与椭圆交于
的直线与椭圆交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 为
为![]() 上一个动点,过点
上一个动点,过点![]() 与椭圆
与椭圆![]() 只有一个公共点的直线为
只有一个公共点的直线为![]() ,过点
,过点![]() 与
与![]() 垂直的直线为
垂直的直线为![]() ,求证:
,求证:![]() 与
与![]() 的交点在定直线上,并求出该定直线的方程.
的交点在定直线上,并求出该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从![]() 种服装商品,
种服装商品,![]() 种家电商品,
种家电商品,![]() 种日用商品中,选出
种日用商品中,选出![]() 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的![]() 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高![]() 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有![]() 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为![]() 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是![]() ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则![]() 最少为多少元?
最少为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 过点
过点![]() ,过抛物线E上一点
,过抛物线E上一点![]() 作两直线PM,PN与圆C:
作两直线PM,PN与圆C:![]() 相切,且分别交抛物线E于M、N两点.
相切,且分别交抛物线E于M、N两点.
(1)求抛物线E的方程,并求其焦点坐标和准线方程;
(2)若直线MN的斜率为![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学的甲、乙、丙三名同学参加高校自主招生考试,每位同学彼此独立的从![]() 五所高校中任选2所.
五所高校中任选2所.
(1)求甲、乙、丙三名同学都选![]() 高校的概率;
高校的概率;
(2)若已知甲同学特别喜欢![]() 高校,他必选
高校,他必选![]() 校,另在
校,另在![]() 四校中再随机选1所;而同学乙和丙对五所高校没有偏爱,因此他们每人在五所高校中随机选2所.
四校中再随机选1所;而同学乙和丙对五所高校没有偏爱,因此他们每人在五所高校中随机选2所.
(i)求甲同学选![]() 高校且乙、丙都未选
高校且乙、丙都未选![]() 高校的概率;
高校的概率;
(ii)记![]() 为甲、乙、丙三名同学中选
为甲、乙、丙三名同学中选![]() 高校的人数,求随机变量
高校的人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、点
、点![]() 及抛物线
及抛物线![]() .
.
(1)若直线![]() 过点
过点![]() 及抛物线
及抛物线![]() 上一点
上一点![]() ,当
,当![]() 最大时求直线
最大时求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在点
轴上是否存在点![]() ,使得过点
,使得过点![]() 的任一条直线与抛物线
的任一条直线与抛物线![]() 交于点
交于点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离相等?若存在,求出点
的距离相等?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com