Question

已知双曲线(a＞0,b＞0)的左、右焦点分别为F₁、F₂,P为双曲线左支上一点,P到左准线的距离为d且d、|PF₁|、|PF₂|成等比数列.

(1)若y=3x是已知双曲线的一条渐近线,求P点的坐标;

(2)求此双曲线离心率e的取值范围.

Answer 1

解:(1)因双曲线的一条渐近线的方程为y=x,故,即b=a.且半焦距c==2a,离心率e=2.

设点P的坐标为(x₀,y₀).

∵d、|PF₁|、|PF₂|成等比数列,

∴

∴|PF₂|=2|PF₁|,|PF₁|=2d.

又∵|PF₂|-|PF₁|=2a,故|PF₁|=2a,

∴a=d.

∴|x₀|=|d+|=|a+|=a.

∵x₀＜0,则x₀=-a.

∵P(x₀,y₀)在双曲线上,∴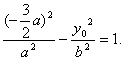

∴y₀=±a.

∴P点的坐标为(-a,±a).

(2)由题设知(e＞1),

∴

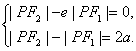
∴|PF₁|=,|PF₂|=.

∵|PF₁|+|PF₂|≥|F₁F₂|=2c=2ea,

∵,又∵a＞0,e＞1,

∴1+e≥e²-ee²-2e-1≤0.∴1＜e≤1+.