
(1)若椭圆上的点M(1,![]() )到F1、F2的距离之和为4,求椭圆方程;
)到F1、F2的距离之和为4,求椭圆方程;
(2)有一个猜想:“设P(x1,y1)、Q(x2,y2)(y1y2≠0)是椭圆C上的任意两点,若P、F1、Q三点共线,则直线PA1、QA2、l共点.”你认为这个猜想能成立吗?请说明理由.
解:(1)由已知得,
2a=|MF1|+|MF2|=4,
∴a=2.又M在椭圆上,
∴![]() +
+![]() =1.
=1.
∴b=![]() .
.
∴椭圆方程为![]() +
+![]() =1.
=1.
(2)由已知,A1(-a,0)、A2(a,0)、F1(-c,0),直线PA1的方程为y=![]() (x+a),
(x+a),
直线QA2的方程为y=![]() (x-a).
(x-a).
设直线PA1与l交于点P′(-![]() ,yP′);直线QA2与直线l交于Q′(-
,yP′);直线QA2与直线l交于Q′(-![]() ,yQ′).
,yQ′).
yP′=![]() (-
(-![]() +a),
+a),
yQ′=![]() (-
(-![]() -a).
-a).
要证PA1、QA2、l共点,只需证yP′=yQ′.
∵P、F1、Q三点共线,
∴![]() =
=![]() .
.
∴c=![]() . ①
. ①
由yP′=yQ′![]()
![]() (-
(-![]() +a)=
+a)=![]() (-
(-![]() -a)
-a)![]()
![]() =
=![]() ,
,
将①代入得yP′=yQ′![]()
![]() . ②
. ②
又∵点P、Q在椭圆C上,
∴
∴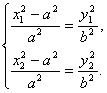
两式相比得![]() ,
,
∴②恒成立.
∴恒有yP′=yQ′.
∴直线PA1、QA2、l恒共点.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
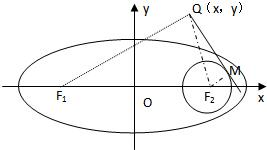 设F1,F2分别是椭圆C:
设F1,F2分别是椭圆C:| x2 |
| 6m2 |
| y2 |
| 2m2 |
| PF1 |
| PF |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
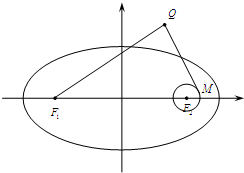 设F1、F2分别是椭圆C:
设F1、F2分别是椭圆C:| x2 |
| 6m2 |
| y2 |
| 2m2 |
| pF1 |
| pF |
| pF1 |
| pF |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| x2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com