
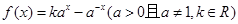 ,
,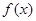 是定义域为
是定义域为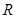 的奇函数.
的奇函数.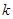 的值,判断并证明当
的值,判断并证明当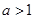 时,函数
时,函数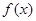 在
在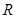 上的单调性;
上的单调性;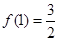 ,函数
,函数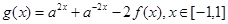 ,求
,求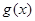 的值域;
的值域;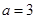 ,若
,若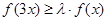 对于
对于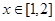 时恒成立.请求出最大的整数
时恒成立.请求出最大的整数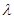 .
.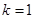 ,
,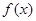 在R上为增函数;(Ⅱ)
在R上为增函数;(Ⅱ)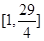 ;(Ⅲ)
;(Ⅲ)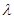 的最大整数为10.
的最大整数为10.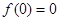 得
得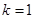 ,由单调性的定义证明
,由单调性的定义证明 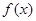 在R上是增函数;
在R上是增函数;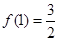 可得
可得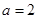 ,
,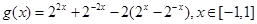 ,由换元法令
,由换元法令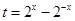 ,将函数转化为二次函数
,将函数转化为二次函数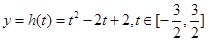 求最值;(Ⅲ)
求最值;(Ⅲ)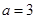 时,原式可化为
时,原式可化为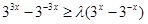 ,令
,令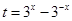 ,由分离参数的方法得到
,由分离参数的方法得到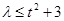 ,进而得到
,进而得到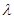 的取值范围.本题中用到换元法,换元之后应特别注意变元
的取值范围.本题中用到换元法,换元之后应特别注意变元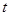 的取值范围.
的取值范围.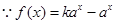 是定义域为R上的奇函数,
是定义域为R上的奇函数,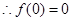 ,得
,得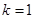 .
.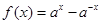 ,
,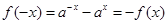 ,即
,即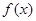 是R上的奇函数 2分
是R上的奇函数 2分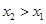 ,则
,则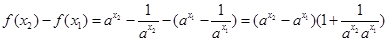 ,
,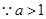 ,
,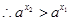 ,
,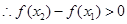 ,
,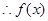 在R上为增函数 5分
在R上为增函数 5分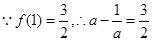 ,即
,即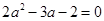 ,
,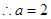 或
或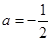 (舍去)
(舍去)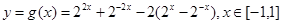 ,令
,令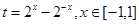 ,
,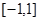 上为增函数,则
上为增函数,则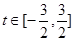
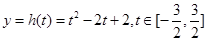 8分
8分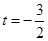 时,
时,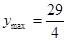 ;当
;当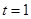 时,
时,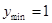
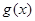 的值域为
的值域为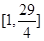 10分
10分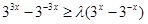 ,在
,在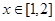 时恒成立
时恒成立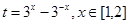 ,则
,则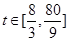
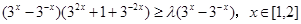 恒成立
恒成立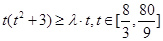 恒成立 13分
恒成立 13分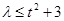 ,
,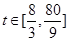 恒成立,当
恒成立,当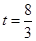 时,
时,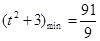
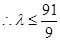 ,则
,则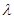 的最大整数为10 16分
的最大整数为10 16分

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com