解:(1)f(x)=x
3-2ax
2+a
2x 令f'(x)=3x
2-4ax+a
2=0,
得:x
1=

,x
2=a.(2分)
1° 当a>0 时,x
1<x
2 ∴所求单调增区间是
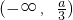
,(a,+∞),单调减区间是(

,a )
2° 当a<0 时,所求单调增区间是(-∞,a),
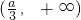
,单调减区间是(a,

)
3° 当a=0 时,f'(x)=3x
2≥0 所求单调增区间是(-∞,+∞).(5分)
(2)f(x)=x
3-(a+b)x
2+abx∴f'(x)=3x
2-2(a+b)x+ab,
∵当x∈[-1,1]时,恒有|f'(x)|≤

∴-

,(8分)即
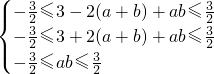
得
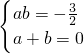
此时,满足当x
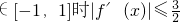
恒成立.
∴
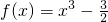
x.(10分)
(3)存在a,b,使得
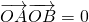
,则m•n+f(m)•f(n)=0
∴mn+mn(m-a)(m-b)(n-a)(n-b)=0由于0<a<b,知mn≠0
∴(m-a)(m-b)(n-a)(n-b)=-1<BR>①由题设,m,n是f'(x)=0的两根
∴
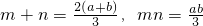
②(12分)②代入①得:ab(a-b)
2=9
∴
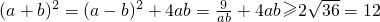
,当且仅当
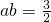
时取“=”
∴

∵a+b≤2

∴
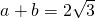
又∵ab=
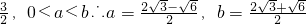
.(16分)
分析:(1)由已知可得f'(x)=3x
2-4ax+a
2=0得:x
1=

,x
2=a,要比较a与,

的大小,故需分a>0,a<0 时,a=0 三种情况讨论,进行求解函数的单调区间
(2)由于f'(x)=3x
2-2(a+b)x+ab,当x∈[-1,1]时,恒有|f'(x)|≤

可得-

,代入可求a,b的关系及函数的解析式
(3)假设存在a,b,使得
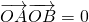
,则可得m•n+f(m)•f(n)=0,由题设,m,n是f'(x)=0的两根,代入可得ab(a-b)
2=9,结合基本不等式可求
点评:本题以结合函数的导数知识:导数与函数的单调性、导数与函数的极值,考查了函数的恒成立问题的转化,属于函数知识的综合应用.

 恒成立,求函数f(x)的表达式;
恒成立,求函数f(x)的表达式; .问:是否存在常数a、b,使得
.问:是否存在常数a、b,使得 •
• =0?若存在,求出a,b的值;若不存在,请说明理由.
=0?若存在,求出a,b的值;若不存在,请说明理由. ,x2=a.(2分)
,x2=a.(2分)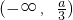 ,(a,+∞),单调减区间是(
,(a,+∞),单调减区间是( ,a )
,a ) 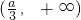 ,单调减区间是(a,
,单调减区间是(a, )
) ∴-
∴- ,(8分)即
,(8分)即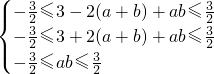 得
得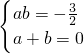
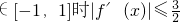 恒成立.
恒成立.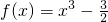 x.(10分)
x.(10分)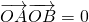 ,则m•n+f(m)•f(n)=0
,则m•n+f(m)•f(n)=0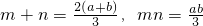 ②(12分)②代入①得:ab(a-b)2=9
②(12分)②代入①得:ab(a-b)2=9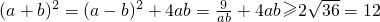 ,当且仅当
,当且仅当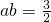 时取“=”
时取“=” ∵a+b≤2
∵a+b≤2 ∴
∴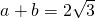
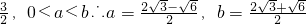 .(16分)
.(16分) ,x2=a,要比较a与,
,x2=a,要比较a与, 的大小,故需分a>0,a<0 时,a=0 三种情况讨论,进行求解函数的单调区间
的大小,故需分a>0,a<0 时,a=0 三种情况讨论,进行求解函数的单调区间
 ,代入可求a,b的关系及函数的解析式
,代入可求a,b的关系及函数的解析式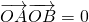 ,则可得m•n+f(m)•f(n)=0,由题设,m,n是f'(x)=0的两根,代入可得ab(a-b)2=9,结合基本不等式可求
,则可得m•n+f(m)•f(n)=0,由题设,m,n是f'(x)=0的两根,代入可得ab(a-b)2=9,结合基本不等式可求

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<