
在四棱锥 中,底面
中,底面 是矩形,已知
是矩形,已知 ,
, ,
, ,
, ,
, 。
。
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的正切值的大小。(12分)
的正切值的大小。(12分)

(1)见解析;(2)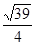 .
.
【解析】第一问中,利用线面垂直的判定定理求证。在 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,
PD=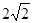 ,可得
,可得 ,于是
,于是
在矩形ABCD中,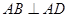 ,又
,又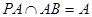
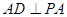 ,从而得到结论。
,从而得到结论。
第二问中,过点P作 于H,过点H作
于H,过点H作 于E,
于E,
连接PE,又因为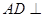 平面PAB,
平面PAB, 平面PAB,所以
平面PAB,所以 ,
,
又 ,因而
,因而 平面ABCD,
平面ABCD,
故HE为PE在平面ABCD内的射影, ,从而得到二面角的平面角
,从而得到二面角的平面角 是二面角P-BD-A的平面角,然后借助于三角形求解得到。
是二面角P-BD-A的平面角,然后借助于三角形求解得到。
解:(I)在 中,由题设PA=2,AD=2,
中,由题设PA=2,AD=2,
PD=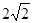 ,可得
,可得 ,
,
于是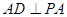 ,……….2分,
,……….2分,
在矩形ABCD中,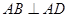 ,又
,又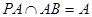 ….4分,
….4分,
所以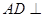 平面PAB。……….6分,
平面PAB。……….6分,
(II)如图所示,过点P作 于H,过点H作
于H,过点H作 于E,
于E,
连接PE,……….7分,
因为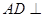 平面PAB,
平面PAB, 平面PAB,所以
平面PAB,所以 ,
,
又 ,因而
,因而 平面ABCD,
平面ABCD,
故HE为PE在平面ABCD内的射影, ,……….8分,
,……….8分,
从而 是二面角P-BD-A的平面角。……….9分,
是二面角P-BD-A的平面角。……….9分,
由题设可得 ,
, ,
,
 ,……….10分,
,……….10分,
由 ~
~ 得
得
 ,于是在
,于是在 中,
中,
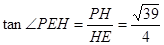 ,….11分,
,….11分,
所以二面角P—BD—A 的正切值的大小为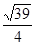 。………….12分
。………….12分


科目:高中数学 来源: 题型:
(2009江西卷文)(本小题满分12分)
如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() .以
.以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成的角;
所成的角;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
(2009江西卷理)(本小题满分12分)
在四棱锥![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() . 以
. 以![]() 的中点
的中点![]() 为球心、
为球心、![]() 为直径的球面交
为直径的球面交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:平面![]() ⊥平面
⊥平面![]() ;
; ![]()
![]()
(2)求直线![]() 与平面
与平面![]() 所成的角的大小;
所成的角的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源:2014届河南省方城一高高三第一次调研(月考)考试理科数学试卷(解析版) 题型:解答题
已知在四棱锥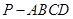 中,底面
中,底面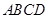 是矩形,
是矩形,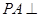 平面
平面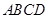 ,
,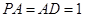 ,
,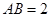 ,
,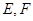 分别是
分别是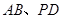 的中点.
的中点.
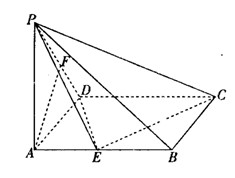
(1)求证: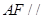 平面
平面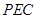 ;
;
(2)求二面角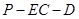 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省五市高三第三次调研测试数学试卷(解析版) 题型:解答题
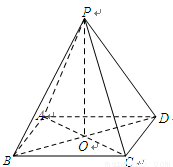
如图,在四棱锥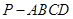 中,底面
中,底面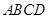 是矩形,四条侧棱长均相等.
是矩形,四条侧棱长均相等.
(1)求证: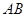
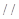 平面
平面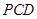 ;
;
(2)求证:平面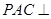 平面
平面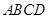 .
.
查看答案和解析>>
科目:高中数学 来源:2014届广东汕头达濠中学高二上期末理科数学试卷(解析版) 题型:解答题
(本小题满分16分)
如图,在四棱锥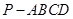 中,底面
中,底面 是矩形,
是矩形,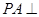 平面
平面 ,
,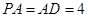 ,
,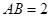 .以
.以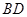 的中点
的中点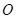 为球心、
为球心、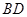 为直径的球面切
为直径的球面切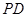 于点
于点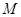 .
.

(1)求证:PD⊥平面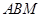 ;
;
(2)求直线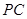 与平面
与平面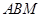 所成的角的正弦值;
所成的角的正弦值;
(3)求点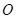 到平面
到平面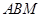 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com