练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设椭圆 ()的左、右焦点分别为，过的直线交椭圆于，两点，若椭圆的离心率为，的周长为.

    (1)求椭圆的方程；

    (2)设不经过椭圆的中心而平行于弦的直线交椭圆于点，，设弦，的中点分别为，证明：三点共线.

    【答案】(Ⅰ) (Ⅱ)详见解析

    【解析】

    (Ⅰ)由的周长为求得，由离心率求得，从而可得的值，进而可得结果；(Ⅱ)易知，当直线的斜率不存在时，三点共线；当直线的斜率存在时，由点差法可得 ，，即，.同理可得，从而可得结论.

    (Ⅰ)由题意知，.

    又∵，∴，，

    ∴椭圆的方程为.

    (Ⅱ)易知，当直线的斜率不存在时，由椭圆的对称性知，中点在轴上，三点共线；

    当直线的斜率存在时，设其斜率为，且设.

    联立方程得相减得，

    ∴，

    ∴，，即，

    ∴.

    同理可得，∴，所以三点共线.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“吸烟有害健康，吸烟会对身体造成伤害”，哈尔滨市于2012年5月31日规定室内场所禁止吸烟．美国癌症协会研究表明，开始吸烟年龄X分别为16岁、18岁、20岁和22岁者，其得肺癌的相对危险度Y依次为15.10，12.81，9.72，3.21；每天吸烟支数U分别为10，20，30者，其得肺癌的相对危险度V分别为7.5，9.5和16.6，用表示变量X与Y之间的线性相关系数，用r2表示变量U与V之间的线性相关系数，则下列说法正确的是(　　)

    A.r1＝r2B.r1＞r2＞0

    C.0＜r1＜r2D.r1＜0＜r2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若四面体的六条棱长分别为2,3,4,5, 6,7,则不同的形状有______种(若两个四面体经适当放置后可完全重合,则认为是相同的形状).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝xln x－aex(e为自然对数的底数)有两个极值点，则实数a的取值范围是(　　)

    A. B.(0，e)

    C. D.(－∞，e)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费 (单位：千元)对年销售量 (单位： )和年利润 (单位：千元)的影响.对近年的年宣传费 和年销售量数据作了初步处理，得到下面的散点图及一些统计量的值.

    表中 ， .附：对于一组数据 ， ， ， ，其回归直线 的斜率和截距的最小二乘法估计分别为 ， .

    （1）根据散点图判断， 与 在哪一个适宜作为年销售量 关于年宣传费 的回归方程类型？(给出判断即可，不必说明理由)

    （2）根据1小问的判断结果及表中数据，建立 关于 的回归方程；

    （3）已知这种产品的年利润 与 的关系为 .根据2小问的结果回答下列问题：

    ①2年宣传费 时，年销售量及年利润的预报值是多少？

    ②3年宣传费为何值时，年利润的预报值最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    某学校用简单随机抽样方法抽取了100名同学，对其日均课外阅读时间（单位：分钟）进行调查，结果如下：

    t

    男同学人数

    7

    11

    15

    12

    2

    1

    女同学人数

    8

    9

    17

    13

    3

    2

    若将日均课外阅读时间不低于60分钟的学生称为“读书迷”.

    （1）将频率视为概率，估计该校4000名学生中“读书迷”有多少人？

    （2）从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.

    （i）求抽取的4位同学中既有男同学又有女同学的概率；

    （ii）记抽取的“读书迷”中男生人数为，求的分布列和数学期望

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】甲、乙、丙三家企业产品的成本分别为10000，12000，15000，其成本构成如下图所示，则关于这三家企业下列说法错误的是（ ）

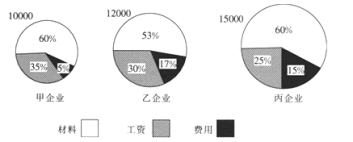
    A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业

    C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】等边的边长为3，点分别为上的点，且满足（如图1），将沿折起到的位置，使二面角成直二面角，连接， （如图2）

    （1）求证： 平面；

    （2）在线段上是否存在点，使直线与平面所成的角为？若存在，求出的长；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，曲线的普通方程为，曲线的参数方程为（为参数），以坐标原点为极点，轴正半轴为极轴建立极坐标系，直线的极坐标方程为.

    （1）求曲线的极坐标方程和曲线的普通方程；

    （2）直线与曲线在第一象限内的交点为，过点的直线交曲线于两点，且的中点为，求直线的斜率.

    查看答案和解析>>

    同步练习册答案