
【题目】已知抛物线y2=4 ![]() x的焦点为F,A、B为抛物线上两点,若
x的焦点为F,A、B为抛物线上两点,若 ![]() =3
=3 ![]() ,O为坐标原点,则△AOB的面积为( )
,O为坐标原点,则△AOB的面积为( )
A.8 ![]()
B.4 ![]()
C.2 ![]()
D.![]()
【答案】B
【解析】解:抛物线y2=4 ![]() x的焦点为F(
x的焦点为F( ![]() ,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
,0),由抛物线的定义可知:|AF|=|AD|,|BC|=|BF|,
过B做BE⊥AD,
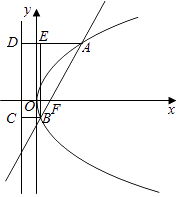
由 ![]() =3
=3 ![]() ,则丨
,则丨 ![]() 丨=丨
丨=丨 ![]() 丨,
丨,
∴|AB|=2|AE|,由抛物线的对称性,不妨设直线的斜率为正,
∴直线AB的倾斜角为60°,直线AB的方程为y= ![]() (x﹣
(x﹣ ![]() )=
)= ![]() x﹣3,
x﹣3,
联立直线AB与抛物线的方程可得: ![]() ,整理得:3x2﹣10
,整理得:3x2﹣10 ![]() x+9=0,
x+9=0,
由韦达定理可知:x1+x2= ![]() ,则丨AB丨=x1+x2+p=
,则丨AB丨=x1+x2+p= ![]() +2
+2 ![]() =
= ![]() ,
,
而原点到直线AB的距离为d= ![]() =
= ![]() ,
,
则三角形△AOB的面积S= ![]() 丨AB丨d=
丨AB丨d= ![]()
![]()
![]() =4
=4 ![]() ,
,
∴当直线AB的倾斜角为120°时,同理可求S=4 ![]() ,
,
所以答案是:B.


科目:高中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() AD与BC交于点M,设
AD与BC交于点M,设![]() ,以
,以![]() 、
、![]() 为基底表示
为基底表示![]()

【答案】![]()
【解析】试题分析:由A、M、D三点共线,知![]() ;由C、M、B三点共线,知
;由C、M、B三点共线,知![]()
,所以 ,所以
,所以![]() =
=![]() .
.
试题解析:
设![]() ,
,
则![]()
因为A、M、D三点共线,所以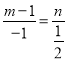 ,即
,即![]()
又![]()
因为C、M、B三点共线,所以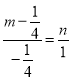 ,即
,即![]()
由![]() 解得
解得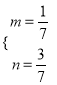 ,所以
,所以![]()
【题型】解答题
【结束】
20
【题目】函数![]() 的最小值为
的最小值为![]() .
.
(1)求![]() ;
;
(2)若![]() ,求
,求![]() 及此时
及此时![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C1的参数方程为 ![]() (θ为参数),曲线 C2的极坐标方程为ρcosθ﹣
(θ为参数),曲线 C2的极坐标方程为ρcosθ﹣ ![]() ρsinθ﹣4=0.
ρsinθ﹣4=0.
(1)求曲线C1的普通方程和曲线 C2的直角坐标方程;
(2)设P为曲线C1上一点,Q为曲线 C2上一点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①若![]() ,
, ![]() 是第一象限角且
是第一象限角且![]() ,则
,则![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③![]() 是函数
是函数![]() 的一条对称轴;
的一条对称轴;
④函数![]() 的图象关于点
的图象关于点![]() 成中心对称;
成中心对称;
⑤设![]() ,则函数
,则函数![]() 的最小值是
的最小值是![]() ,其中正确命题的序号为 __________.
,其中正确命题的序号为 __________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)=ex+mx2﹣m(m>0),当x1+x2=1时,不等式f(x1)+f(0)>f(x2)+f(1)恒成立,则实数x1的取值范围是( )
A.(﹣∞,0)
B.![]()
C.![]()
D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列{an}的首项a1=1,且(n+1)a ![]() +anan+1﹣na
+anan+1﹣na ![]() =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;、
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业招聘中,依次进行A科、B科考试,当A科合格时,才可考B科,且两科均有一次补考机会,两科都合格方通过.甲参加招聘,已知他每次考A科合格的概率均为 ![]() ,每次考B科合格的概率均为
,每次考B科合格的概率均为 ![]() .假设他不放弃每次考试机会,且每次考试互不影响.
.假设他不放弃每次考试机会,且每次考试互不影响.
(I)求甲恰好3次考试通过的概率;
(II)记甲参加考试的次数为ξ,求ξ的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 ![]() 和
和 ![]() ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(1)两种大树各成活1株的概率;
(2)成活的株数ξ的分布列与期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com