
 .
.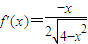 .
.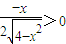 ,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);
,解得-2<x<0,所以函数f(x)的递增区间是(-2,0);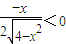 ,解得0<x<2,所以函数f(x)的递减区间是(0,2).
,解得0<x<2,所以函数f(x)的递减区间是(0,2).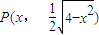 ,则切线的斜率
,则切线的斜率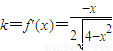 ,
,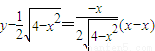 ,
,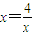 ,所以
,所以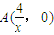 ;
;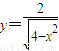 ,所以
,所以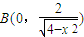 ,
,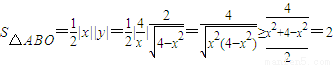 ,
,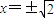 时,△ABO面积的最小值为2.
时,△ABO面积的最小值为2.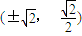 .
.

 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源:2011年高三数学第一轮基础知识训练(24)(解析版) 题型:解答题
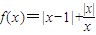 .
.查看答案和解析>>
科目:高中数学 来源:2014届湖南省高二下学期第一次月考数学试卷(解析版) 题型:解答题
已知函数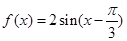 ,
,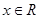 .
.
(1)写出函数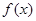 的周期;
的周期;
(2)将函数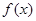 图象上的所有的点向左平行移动
图象上的所有的点向左平行移动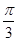 个单位,得到函数
个单位,得到函数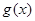 的图象,写出函数
的图象,写出函数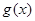 的表达式,并判断函数
的表达式,并判断函数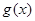 的奇偶性.
的奇偶性.
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期期中考试数学试卷(解析版) 题型:解答题
(12分)已知函数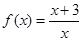 :
:
(1)写出此函数的定义域和值域;
(2)证明函数在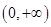 为单调递减函数;
为单调递减函数;
(3)试判断并证明函数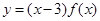 的奇偶性.
的奇偶性.
查看答案和解析>>
科目:高中数学 来源:2014届福建省厦门市高一第一学期期中数学试卷 题型:解答题
已知函数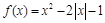 的图像,并写出该函数的单调区间与值域。
的图像,并写出该函数的单调区间与值域。
(1)利用绝对值及分段函数知识,将函数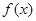 的解析式写成分段函数;
的解析式写成分段函数;
(2)在给出的坐标系中画出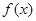 的图象,并根据图象写出函数
的图象,并根据图象写出函数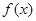 的单调区间和值域.
的单调区间和值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com