
过抛物线C: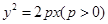 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
(1)求抛物线C的方程及点M的坐标;
(2)过点M作倾斜角互补的两条直线分别与抛物线C交于A,B两点,且直线AB过点(0,-1),求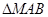 的面积.
的面积.
(1)y2=8x,(2,4);(2)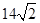 .
.
解析试题分析:本题主要考查抛物线的标准方程及其几何性质、韦达定理、点到直线的距离、三角形面积公式等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,由题意结合抛物线图象得到M点坐标,代入抛物线方程中,解出P的值,从而得到抛物线的标准方程及M点坐标;第二问,设出A,B点坐标,利用M点,分别得到直线MA和直线MB的斜率,因为两直线倾斜角互补,所以两直线的斜率相加为0,整理得到y1+y2=-8,代入到 中得到直线AB的斜率,于是得到直线AB的方程,令直线与抛物线联立,得到
中得到直线AB的斜率,于是得到直线AB的方程,令直线与抛物线联立,得到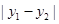 ,而
,而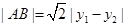 ,
,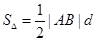 ,而
,而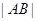 用两点间距离公式转化,d是M到直线AB的距离,从而得到
用两点间距离公式转化,d是M到直线AB的距离,从而得到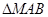 的面积.
的面积.
(1)抛物线C的准线x=-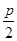 ,依题意M(4-
,依题意M(4-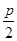 ,4),
,4),
则42=2p(4-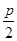 ),解得p=4.
),解得p=4.
故抛物线C的方程为y2=8x,点M的坐标为(2,4), 3分
(2)设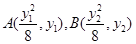 .
.
直线MA的斜率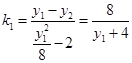 ,同理直线MB的斜率
,同理直线MB的斜率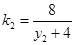 .
.
由题设有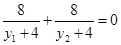 ,整理得y1+y2=-8.
,整理得y1+y2=-8.
直线AB的斜率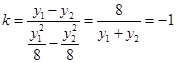 . 6分
. 6分
于是直线AB的方程为y=-x-1.
由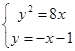 得y2+8y+8=0.
得y2+8y+8=0.
|y1-y2|=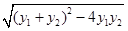 =
= ,
,
于是|AB|=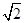 |y1-y2|=8. 10分
|y1-y2|=8. 10分
点M到直线AB的距离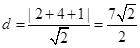 ,
,
则△MAB的面积S=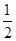 |AB|·d=
|AB|·d=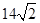 . 12分
. 12分
考点:抛物线的标准方程及其几何性质、韦达定理、点到直线的距离、三角形面积公式.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知点A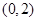 ,椭圆E:
,椭圆E: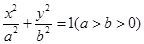 的离心率为
的离心率为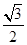 ;F是椭圆E的右焦点,直线AF的斜率为
;F是椭圆E的右焦点,直线AF的斜率为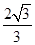 ,O为坐标原点
,O为坐标原点
(I)求E的方程;
(II)设过点A的动直线 与E 相交于P,Q两点。当
与E 相交于P,Q两点。当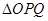 的面积最大时,求
的面积最大时,求 的直线方程.
的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设抛物线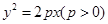 的焦点为
的焦点为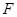 ,点
,点 ,线段
,线段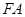 的中点在抛物线上.设动直线
的中点在抛物线上.设动直线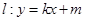 与抛物线相切于点
与抛物线相切于点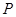 ,且与抛物线的准线相交于点
,且与抛物线的准线相交于点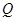 ,以
,以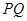 为直径的圆记为圆
为直径的圆记为圆 .
.
(1)求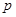 的值;
的值;
(2)证明:圆 与
与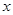 轴必有公共点;
轴必有公共点;
(3)在坐标平面上是否存在定点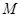 ,使得圆
,使得圆 恒过点
恒过点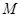 ?若存在,求出
?若存在,求出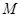 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆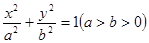 的右焦点为
的右焦点为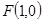 ,离心率
,离心率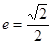 ,
,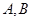 是椭圆上的动点.
是椭圆上的动点.
(1)求椭圆标准方程;
(2)若直线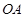 与
与 的斜率乘积
的斜率乘积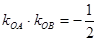 ,动点
,动点 满足
满足 ,(其中实数
,(其中实数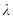 为常数).问是否存在两个定点
为常数).问是否存在两个定点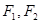 ,使得
,使得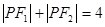 ?若存在,求
?若存在,求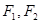 的坐标及
的坐标及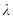 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(13分)(2011•天津)设椭圆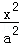 +
+ =1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|.
(Ⅰ)求椭圆的离心率e;
(Ⅱ)设直线PF2与椭圆相交于A,B两点,若直线PF2与圆(x+1)2+ =16相交于M,N两点,且|MN|=
=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆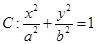
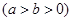 的离心率为
的离心率为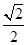 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线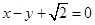 相切.
相切.
(1)求椭圆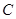 的方程;
的方程;
(2)若过点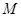 (2,0)的直线与椭圆
(2,0)的直线与椭圆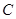 相交于两点
相交于两点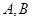 ,设
,设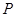 为椭圆上一点,且满足
为椭圆上一点,且满足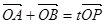 (
(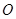 为坐标原点),当
为坐标原点),当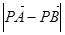 <
<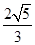 时,求实数
时,求实数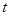 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆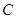 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,右焦点到右顶点的距离为
,右焦点到右顶点的距离为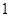 .
.
(Ⅰ)求椭圆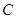 的标准方程;
的标准方程;
(Ⅱ)若直线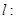
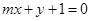 与椭圆
与椭圆 交于
交于 两点,是否存在实数
两点,是否存在实数 ,使
,使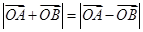 成立?若存在,求
成立?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆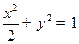 ,
, 为坐标原点,椭圆的右准线与
为坐标原点,椭圆的右准线与 轴的交点是
轴的交点是 .
.
(1)点 在已知椭圆上,动点
在已知椭圆上,动点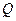 满足
满足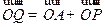 ,求动点
,求动点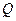 的轨迹方程;
的轨迹方程;
(2)过椭圆右焦点 的直线与椭圆交于点
的直线与椭圆交于点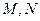 ,求
,求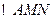 的面积的最大值
的面积的最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com