已知函数f(x)=x3-ax2.
(1)若a=3,求函数f(x)的极大值和极小值;
(2)在(1)的条件下,当k满足什么条件时,方程f(x)+k=0只有两个解;
(3)若函数f(x)的图象的切线过点(0,1),且过该点的切线有两点,求实数a的值.
解:(1)由于a=3,则f(x)=x
3-3x
2,所以f'(x)=3x
2-6x=0,得x
1=0,x
2=2
| x | (-∞,0) | 0 | (0,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 0 | ↘ | -4 | ↗ |
∴f
极大值(x)=f(0)=0f
极小值(x)=f(2)=-4
(2)由(1)得k=0或k=4时只有两解;
(3)∵函数f(x)的图象的切线过点(0,1),且过该点的切线有两条,
∴设切点为(x,x
3-ax
2),又切线过点(0,1),f′(x)=3x
2-2ax,
∴
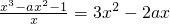
,
化简得2x
3-ax
2+1=0…①,∵有两条切线,
∴方程①只能有两个根,
∵2x
3-ax
2=-1,令h(x)=2x
3-ax
2,y=-1,则h′(x)=6x
2-2ax,令h′(x)=0,解得,x
1=0,x
2=

,
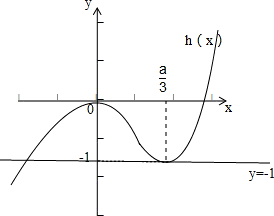
画出h(x)的图象:利用数形结合可得,要是方程①只有两个根,∴h(

)=-1,
∴2×
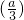 3
3-a×
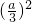
=-1,解得a=3.
分析:(1)把a=3代入函数f(x)=x
3-ax
2,求导,解出极值点,列出表格即可求解;
(2)由(1)的表格,画出草图即可求解;
(3)首先设出切点,根据函数f(x)的图象的切线过点(0,1),且过该点的切线有两条,根据斜率和导数的关系列出方程,可知方程只有两个根,根据数形结合的方法可以求出a值.
点评:此题主要考查例如函数的导数研究函数的极大值和极小值,列出表格可以画出函数的大致草图,此题第三问比较难,利用数形结合的方法求出a的值,难度比较大.


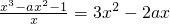 ,
, ,
, )=-1,
)=-1,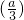 3-a×
3-a×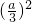 =-1,解得a=3.
=-1,解得a=3.

 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<