
(1)已知点![]() ,
,![]() ,延长AB至C,使
,延长AB至C,使![]() 。求点C
。求点C
的坐标;
(2)已知A![]() ,B
,B![]() 求点C使
求点C使![]() ;
;
(3)已知椭圆两焦点F1![]() ,F2
,F2![]() ,离心率e=0.8。求此椭圆长轴上
,离心率e=0.8。求此椭圆长轴上
两顶点的坐标。
解:(1)![]() 点C在AB延长线上,且
点C在AB延长线上,且![]() ,
,
![]()
![]()
![]() 。
。
设点C坐标为![]() ,
,
则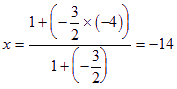
![]()
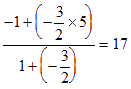 。
。
![]() 点C坐标为
点C坐标为![]() 。
。
(2) 设点![]()
若点C在线段AB上,由![]() 可得
可得![]() ,
,
则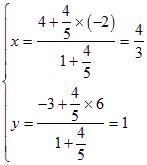
若点C在线段BA的延长线上,由![]() 可得
可得![]() ,
,
则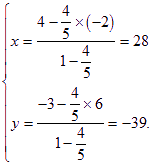
点C坐标为![]() 或
或![]()
(注:点C不可能在线段AB延长线上)
(3)设椭圆的长轴上两顶点A![]() ,A
,A![]() 坐标分别为
坐标分别为![]()
(A![]() 在
在![]() 延长线上,A
延长线上,A![]() 在
在![]() 延长线上)
延长线上)
由椭圆性质可知,
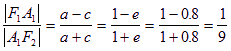
![]()
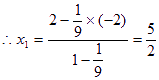
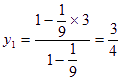
同理,A![]() 分线段
分线段![]() 所成比
所成比![]() 。可得
。可得![]()
![]() 点A
点A![]() ,A
,A![]() 坐标分别为
坐标分别为![]() 。
。
这道题的几个小题都是求线段上的分点的问题。第(1)小题已明确给出C 点的位置,即它在AB的延长线上,且![]() ,因此,可以知道比值
,因此,可以知道比值![]() ,代入线段的定比分点公式即可,对第(2)小题,应注意由
,代入线段的定比分点公式即可,对第(2)小题,应注意由![]() ,还不确定点C是在线段AB上,还是在线段BA的延长线上。因此,解此题时要考虑周到,不要丢解。对于第(3)小题,从题目表面还不能直接看出是求线段的定比分点问题,必须对椭圆的一些基本性质熟练掌握,应想到椭圆的焦点与长轴上两顶点的关系,及离心率的意义,才能给恰当地找出长轴上顶点分线段F1F2所成的比,才能求出长轴上两顶点的坐标。
,还不确定点C是在线段AB上,还是在线段BA的延长线上。因此,解此题时要考虑周到,不要丢解。对于第(3)小题,从题目表面还不能直接看出是求线段的定比分点问题,必须对椭圆的一些基本性质熟练掌握,应想到椭圆的焦点与长轴上两顶点的关系,及离心率的意义,才能给恰当地找出长轴上顶点分线段F1F2所成的比,才能求出长轴上两顶点的坐标。


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中数学 来源: 题型:
 如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
如图,已知点A(-1,0)与点B(1,0),C是圆x2+y2=1上的动点,连接BC并延长至D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题:(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题:(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)| π |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 48 |
| 5 |
| 48 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3π |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com