分析:(I)取AD的中点H,连接EH,则EH⊥平面ABCD,过H作HF⊥AC与F,连接EF,我们可得∠EFH即为二面角E-AC-B的补角,解三角形EFH后,即可求出二面角E-AC-B的正切值;
(II)直线A1C1到平面EAC的距离,即A1点到平面EAC的距离,利用等体积法,我们根据VA1-EAC=VD-A1AE,即可求出直线A1C1到平面EAC的距离.
解答:解:(I)取AD的中点H,连接EH,则EH⊥平面ABCD,过H作HF⊥AC与F,连接EF,
则EF在平面ABCD内的射影为HF,由三垂线定理得EF⊥AC,,
∴∠EFH即为
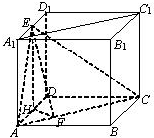
二面角E-AC-B的补角
∵EH=a,HF=
BD=
a∴∠tan∠EFH=
=
=2
∴二面角E-AC-B的正切值为-2
…6分
(II)直线A
1C
1到平面EAC的距离,即A
1点到平面EAC的距离d,…8分
∵
VA1-EAC=
VD-A1AE∴S
△EAC•d=
SA1AE•CD∵EF=
=
=
a∴S
△EAC=
•AC•EF=
•
a•
a=
a2而
SA1AE=
•
•a=
∴
a2•d=
•a
∴d=
∴直线A
1C
1到平面EAC的距离
点评:本题考查的知识点是二面角的平面角及求法,点到平面的距离,其中(I)的关键是得到∠EFH即为二面角E-AC-B的补角,(II)中求点到面的距离时,等体积法是最常用的方法.

 如图所示,在正方体ABCD-A1B1C1D1中,AB=a,E为棱A1D1中点.
如图所示,在正方体ABCD-A1B1C1D1中,AB=a,E为棱A1D1中点. 二面角E-AC-B的补角
二面角E-AC-B的补角

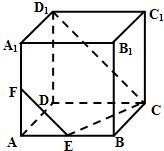 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点 (2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )
(2011•宝山区二模)如图所示,在正方体ABCD-A1B1C1D1的侧面ABB1A1内有一动点P到直线A1B1和直线BC的距离相等,则动点P所在曲线形状为( )