若不等式(1-a)x2-4x+6>0的解集是{x|-3<x<1}.
(1)解不等式2x2+(2-a)x-a>0
(1)b为何值时,ax2+bx+3≥0的解集为R.
【答案】
分析:(1)由不等式(1-a)x
2-4x+6>0的解集是{x|-3<x<1},利用根与系数关系列式求出a的值,把a代入不等式2x
2+(2-a)x-a>0后直接利用因式分解法求解;
(2)代入a得值后,由不等式对应的方程的判别式小于等于0列式求解b的取值范围.
解答:解:(1)由题意知,1-a<0,且-3和1是方程(1-a)x
2-4x+6=0的两根,
∴
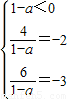
,解得a=3.
∴不等式2x
2+(2-a)x-a>0即为2x
2-x-3>0,解得x<-1或x>

.
∴所求不等式的解集为{x|x<-1或x>

};
(2)ax
2+bx+3≥0即为3x
2+bx+3≥0,
若此不等式的解集为R,则b
2-4×3×3≤0,∴-6≤b≤6.
点评:本题考查了一元二次不等式的解法,考查了一元二次方程的根与系数的关系,是基础的运算题.

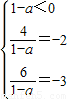 ,解得a=3.
,解得a=3. .
. };
};
