练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数 .
    （1）求函数的单调区间；
    （2）若函数 有两个零点 ,证明 .

    【答案】
    （1）解： , 当 时, ;当 时, ,所以函数 在 上单调递减，在 上单调递增.
    （2）解： ,不妨设 ，又由（1）可知 ，又函数 在 上单调递减，所以 等价于 ，即 .又 ，而 ，所以 ,设 ，则 ，当 时， ，而 ，故当 时， .所以而 恒成立，所以当 时, ,故 .

    【解析】(1)根据题意首先求出原函数的导函数，借助导函数的性质求出原函数的极值点，并判断导函数的正负进而得到原函数的单调性。(2)由已知利用函数 f ( x ) 在 ( ∞ , 1 ) 上单调递减得出x 1 > 2 x 2 ,可转化为 0 = f ( x 1 ) < f ( 2 x 2 ）求出 f ( 2 x 2 ）的解析式，构造函数g ( x )再利用形式函数的导数，讨论导函数的正负进而得出g ( x )的最值，然后转化该式求解即可。
    【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减，以及对函数的最大(小)值与导数的理解，了解求函数在上的最大值与最小值的步骤：（1）求函数在内的极值；（2）将函数的各极值与端点处的函数值，比较，其中最大的是一个最大值，最小的是最小值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在四棱锥P﹣ABCD中，底面ABCD为直角梯形，∠BAD=∠ADC=90°，DC=2AB=2AD，BC⊥PD，E，F分别是PB，BC的中点．
    求证：
    （1）PC∥平面DEF；
    （2）平面PBC⊥平面PBD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线 在 的上方，且曲线 上的任意一点到点 的距离比到直线 的距离都小1.
    （Ⅰ）求曲线 的方程；
    （Ⅱ）设 ，过点 的直线与曲线 相交于 两点.
    ①若 是等边三角形，求实数 的值；
    ②若 ，求实数 的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《中华人民共和国个人所得税》规定，公民月工资、薪金所得不超过3500元的部分不纳税，超过3500元的部分为全月纳税所得额，此项税款按下表分段累计计算：

    已知张先生的月工资、薪金所得为10000元，问他当月应缴纳多少个人所得税？

    设王先生的月工资、薪金所得为元，当月应缴纳个人所得税为元，写出与的函数关系式；

    （3）已知王先生一月份应缴纳个人所得税为303元，那么他当月的个工资、薪金所得为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图像是由函数的图像经如下变换得到：先将图像上所有点的纵坐标伸长到原来的2倍（横坐标不变），再将所得到的图像向右平移个单位长度.

    （Ⅰ）求函数的解析式，并求其图像的对称轴方程；

    （Ⅱ）已知关于的方程在内有两个不同的解．

    （1）求实数m的取值范围；

    （2）证明：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知首项为 的等比数列{an}不是递减数列，其前n项和为Sn （n∈N*），且S3+a3 ， S5+a5 ， S4+a4成等差数列．
    （1）求数列{an}的通项公式；
    （2）若实数a使得a＞Sn+ 对任意n∈N*恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥PABC中，D，E，F分别为棱PC，AC，AB的中点，已知PA⊥AC，PA=6，BC=8，DF=5．求证：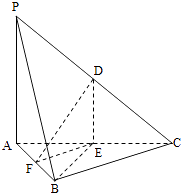

    （1）直线PA∥平面DEF；
    （2）平面BDE⊥平面ABC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ） （A＞0，ω＞0，0＜φ＜π），其导函数f′（x）的部分图象如图所示，则函数f（x）的解析式为（ ）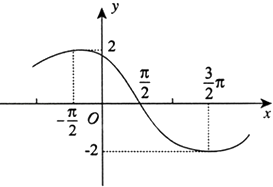
    A.f（x）=4sin（ x+ π）
    B.f（x）=4sin（ x+ ）
    C.f（x）=4sin（ x+ ）
    D.f（x）=4sin（ x+ ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)=x2+4xsinα+tanα(0<a<)有且仅有一个零点

    (Ⅰ)求sin2a的值;

    (Ⅱ)若cos2β+2sin2β=+sinβ, β∈,求β-2α的值

    查看答案和解析>>

    同步练习册答案