
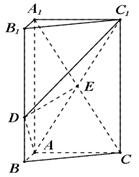
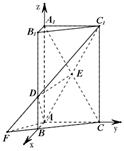
如图,三棱柱 中,
中,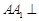 平面
平面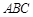 ,
, ,
, , 点
, 点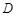 在线段
在线段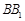 上,且
上,且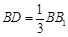 ,
,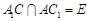 .
.
(Ⅰ)求证:直线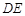 与平面
与平面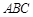 不平行;
不平行;
(Ⅱ)设平面 与平面
与平面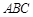 所成的锐二面角为
所成的锐二面角为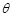 ,若
,若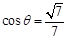 ,求
,求 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面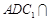 平面
平面 ,求直线
,求直线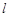 与
与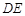 所成的角的余弦值.
所成的角的余弦值.
(Ⅰ)见解析 (Ⅱ) 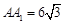 .(Ⅲ)直线
.(Ⅲ)直线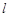 与
与 所成的角的余弦值为
所成的角的余弦值为 .
.
【解析】(I)本小题易用空间向量法解决,易求出平面ABC的法向量,然后证明向量DE与平面ABC的法向量的数量积不等于零即可.
(2)先求出平面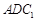 的一个法向量,然后
的一个法向量,然后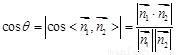 ,可以求出此直棱柱的高.
,可以求出此直棱柱的高.
(3)先找出平面平面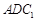 与平面
与平面 的交线.在平面
的交线.在平面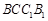 内,分别延长
内,分别延长 ,交于点
,交于点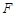 ,连结
,连结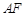 ,则直线
,则直线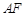 为平面
为平面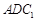 与平面
与平面 的交线.
的交线.
然后求出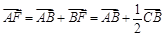 的坐标,再根据
的坐标,再根据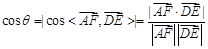 ,求出直线
,求出直线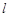 与
与 所成的角的余弦值.
所成的角的余弦值.
依题意,可建立如图所示的空间直角坐标系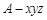 ,设
,设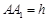 ,则
,则
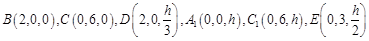 .2分
.2分
(Ⅰ)证明:由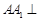 平面
平面 可知
可知 为平面
为平面 的一个法向量.
的一个法向量.
∴ 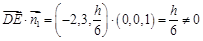 .∴ 直线
.∴ 直线 与平面
与平面 不平行. 4分
不平行. 4分
(Ⅱ)设平面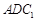 的法向量为
的法向量为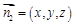 ,则
,则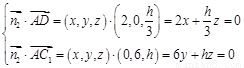 ,
,
取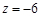 ,则
,则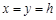 ,故
,故 .6分
.6分
∴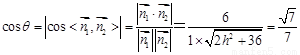 ,7分解得
,7分解得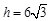 .∴
.∴ 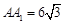 .
.
(Ⅲ)在平面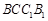 内,分别延长
内,分别延长 ,交于点
,交于点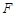 ,连结
,连结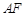 ,则直线
,则直线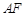 为平面
为平面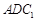 与平面
与平面 的交线.∵
的交线.∵ 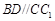 ,
,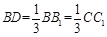 ,∴
,∴ 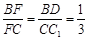 .∴
.∴ 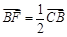 ,
,
∴  .········ 11分
.········ 11分
由(Ⅱ)知,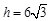 ,故
,故 ,
,
∴  .∴ 直线
.∴ 直线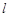 与
与 所成的角的余弦值为
所成的角的余弦值为


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
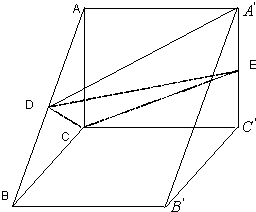 如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点
如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东湛江市普通高考测试卷(一)理科数学试卷(解析版) 题型:解答题
如图,三棱柱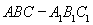 中,△ABC是正三角形,
中,△ABC是正三角形,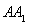
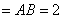 ,平面
,平面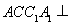 平面
平面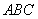 ,
,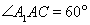 .
.
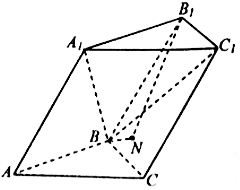
(1)证明: ;
;
(2)证明:求二面角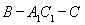 的余弦值;
的余弦值;
(3)设点 是平面
是平面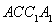 内的动点,求
内的动点,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
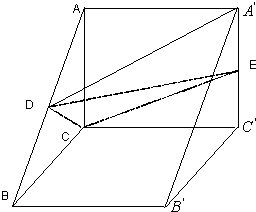 如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点
如图,三棱柱中,平面AC′⊥面BB′C′C,∠CC′B′=60°,BC=CC′AC=2,点D、E分别为棱AB,A′C′的中点查看答案和解析>>
科目:高中数学 来源:2012年东北三省三校高考数学二模试卷(文科)(解析版) 题型:解答题
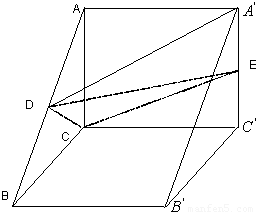
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com