练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，已知多面体中，四边形为菱形，为正四面体，且.

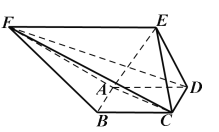
    （1）求证：平面；

    （2）求二面角的余弦值.

    【答案】（1）证明见解析（2）

    【解析】

    （1）通过证明平面平面来证明平面；

    （2）如图，以菱形的两条对角线所在直线分别为x，y轴建立空间直角坐标系，利用向量法计算二面角的余弦值.

    （1）证明：因为四边形为菱形，

    所以，

    又平面，平面，所以平面，

    同理可得平面，

    因为平面，，

    所以平面平面

    因为平面，所以平面.

    （2）以菱形的两条对角线所在直线分别为x，y轴建立空间直角坐标系，如图所示：

    设，则，

    因为为正四面体，所以点E坐标为，

    ，

    因为平面平面，

    所以平面与平面的法向量相同.

    设平面的一个法向量为，则

    ，即

    可取.

    可取为平面的法向量.

    所以，

    所以二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的方程为，斜率为的直线与椭圆交于，两点，点在直线的左上方．

    （1）若以为直径的圆恰好经过椭圆右焦点，求此时直线的方程；

    （2）求证：的内切圆的圆心在定直线上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有甲、乙、丙、丁、戊5种在线教学软件，若某学校要从中随机选取3种作为教师“停课不停学”的教学工具，则其中甲、乙、丙至多有2种被选取的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（1）已知f(x)＝x3＋3ax2＋bx＋a2在x＝－1时有极值0，求常数a，b的值；

    （2）设函数g(x)＝x3－6x＋5，x∈R. 若关于x的方程g(x)＝m有三个不同的实根，求实数m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着运动app和手环的普及和应用，在朋友圈、运动圈中出现了每天1万步的健身打卡现象，“日行一万步，健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友（共500人）的走路步数，并整理成下表：

    分组（单位：千步）

    频数

    60

    240

    100

    60

    20

    18

    0

    2

    （1）请估算这一天小王朋友圈中好友走路步数的平均数（同一组中数据以这组数据所在区间中点值作代表）；

    （2）若用表示事件“走路步数低于平均步数”，试估计事件发生的概率；

    （3）若称每天走路不少于8千步的人为“健步达人”，小王朋友圈中岁数在40岁以上的中老年人共有300人，其中健步达人恰有150人，请填写下面列联表.根据列联表判断，有多大把握认为，健步达人与年龄有关？

    健步达人

    非健步达人

    合计

    40岁以上

    不超过40岁

    合计

    附：.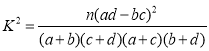

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，边长为a的空间四边形ABCD中，∠BCD＝90°，平面ABD⊥平面BCD，则异面直线AD与BC所成角的大小为（　　）

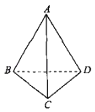
    A. 30°B. 45°C. 60°D. 90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，为抛物线上不同的两点，且，点且于点.

    （1）求的值；

    （2）过轴上一点 的直线交于，两点，在的准线上的射影分别为，为的焦点，若，求中点的轨迹方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1＝1，an＝(n∈N*，n≥2)，数列{bn}满足关系式bn＝(n∈N*)．

    (1)求证：数列{bn}为等差数列；

    (2)求数列{an}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以原点为极点，轴正半轴为极轴建立极坐标系．已知直线的极坐标方程为，曲线的极坐标方程为．

    （1）写出直线和曲线的直角坐标方程；

    （2）过动点且平行于的直线交曲线于两点，若，求动点到直线的最近距离．

    查看答案和解析>>

    同步练习册答案