
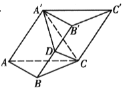
【题目】在三棱柱![]() 中,
中,![]() ,侧面
,侧面![]() 底面
底面![]() ,D是棱
,D是棱![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,根据题意可证四边形
,根据题意可证四边形![]() 是平行四边形,即
是平行四边形,即![]() .根据侧面
.根据侧面![]() 底面
底面![]() ,可得
,可得![]() 平面
平面![]() ,根据面面垂直的判定定理,即可得证。
,根据面面垂直的判定定理,即可得证。
(2)分别以![]() 分别为
分别为![]() 轴正方向建系,求出各点坐标及平面
轴正方向建系,求出各点坐标及平面![]() 和平面
和平面![]() 的法向量,利用面面角的公式求解即可。
的法向量,利用面面角的公式求解即可。

解:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
则![]() 为
为![]() 的中点,
的中点,
因为三棱柱![]() ,
,
所以![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形.
是平行四边形.
又![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() .
.
因为侧面![]() 底面
底面![]() ,且
,且![]() ,
,
所以![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]()
(2)连接![]() ,因为
,因为![]() ,所以
,所以![]() 是等边三角形,故
是等边三角形,故![]() 底面
底面![]() 。
。
设![]() ,可得
,可得![]() ,
,
分别以![]() 分别为
分别为![]() 轴正方向建立空间直角坐标系,
轴正方向建立空间直角坐标系,
则![]()
![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
则![]()
所以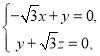 ,取
,取![]()
所以![]()
又平面![]() 的一个法向量为
的一个法向量为![]()
故![]()
因为二面角![]() 为钝角,所以其余弦值为
为钝角,所以其余弦值为![]() .
.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
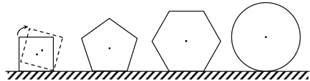
【题目】现有边长均为1的正方形正五边形正六边形及半径为1的圆各一个,在水平桌面上无滑动滚动一周,它们的中心的运动轨迹长分别为![]() ,
,![]() ,
,![]() ,
,![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某公司举行的一次真假游戏的有奖竞猜中,设置了“科技”和“生活”这两类试题,规定每位职工最多竞猜3次,每次竞猜的结果相互独立.猜中一道“科技”类试题得4分,猜中一道“生活”类试题得2分,两类试题猜不中的都得0分.将职工得分逐次累加并用X表示,如果X的值不低于4分就认为通过游戏的竞猜,立即停止竞猜,否则继续竞猜,直到竞猜完3次为止.竞猜的方案有以下两种:方案1:先猜一道“科技”类试题,然后再连猜两道“生活”类试题;
方案2:连猜三道“生活”类试题.
设职工甲猜中一道“科技”类试题的概率为0.5,猜中一道“生活”类试题的概率为0.6.
(1)你认为职工甲选择哪种方案通过竞猜的可能性大?并说明理由.
(2)职工甲选择哪一种方案所得平均分高?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才能:礼乐射御书数,某校国学社团周末开展“六艺”课程讲座活动,每天连排六节,每艺一节,排课有如下要求:“礼”和“数”不能相邻,“射”和“乐”必须相邻,则“六艺”课程讲座不同的排课顺序共有( )
A.24种B.72种C.96种D.144种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
,![]() ,过
,过![]() 的直线与C交于M,N两点,
的直线与C交于M,N两点,![]() 的周长为
的周长为![]() .
.
(1)求椭圆C的标准方程;
(2)过M作与y轴垂直的直线l,点![]() ,试问直线
,试问直线![]() 与直线l交点的横坐标是否为定值?请说明理由.
与直线l交点的横坐标是否为定值?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AB=2,![]() ,D为AC上的一点(不含端点),将△BCD沿直线BD折起,使点C在平面ABD上的射影O在线段AB上,则线段OB的取值范围是( )
,D为AC上的一点(不含端点),将△BCD沿直线BD折起,使点C在平面ABD上的射影O在线段AB上,则线段OB的取值范围是( )
A.(![]() ,1)B.(
,1)B.(![]() ,
,![]() )C.(
)C.(![]() ,1)D.(0,
,1)D.(0,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级有400名学生参加某项体育测试,根据男女学生人数比例,使用分层抽样的方法从中抽取了100名学生,记录他们的分数,将数据分成7组:![]() ,整理得到如下频率分布直方图:
,整理得到如下频率分布直方图:
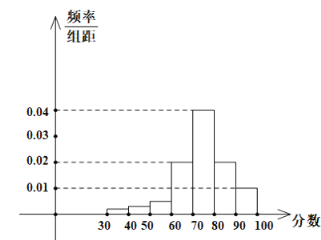
(1)若该样本中男生有55人,试估计该学校高三年级女生总人数;
(2)若规定小于60分为“不及格”,从该学校高三年级学生中随机抽取一人,估计该学生不及格的概率;
(3)若规定分数在![]() 为“良好”,
为“良好”,![]() 为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
为“优秀”.用频率估计概率,从该校高三年级随机抽取三人,记该项测试分数为“良好”或“优秀”的人数为X,求X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com