
【题目】某校在一次期末数学测试中,为统计学生的考试情况,从学校的2000名学生中随机抽取50名学生的考试成绩,被测学生成绩全部介于65分到145分之间(满分150分),将统计结果按如下方式分成八组:第一组![]() ,
,![]() ,第二组
,第二组![]() ,
,![]() ,
,![]() 第八组
第八组![]() ,
,![]() ,如图是按上述分组方法得到的频率分布直方图的一部分.
,如图是按上述分组方法得到的频率分布直方图的一部分.
(1)求第七组的频率,并完成频率分布直方图;
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分(同一组中的数据用该组区间的中点值代表该组数据平均值);
(3)若从样本成绩属于第六组和第八组的所有学生中随机抽取2名,求他们的分差的绝对值小于10分的概率.

【答案】(1)![]() ,绘图见解析;(2)
,绘图见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由频率分布直方图可得:各小矩形的高之和为0.1,运算可得解;
(2)由频率分布直方图中平均数的求法即可得解;
(3)样本成绩属于第六组的有![]() 人,样本成绩属于第八组的有
人,样本成绩属于第八组的有![]() 人,则随机抽取2名,
人,则随机抽取2名,
基本事件总数为![]() ,他们的分差的绝对值小于10分包含的基本事件个数为
,他们的分差的绝对值小于10分包含的基本事件个数为![]() ,再利用古典概型概率公式运算即可.
,再利用古典概型概率公式运算即可.
解:(1)由频率分布直方图得第七组的频率为:
![]() .
.
完成频率分布直方图如下:
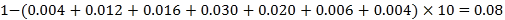
(2)用样本数据估计该校的2000名学生这次考试成绩的平均分为:
![]()
![]() .
.
(3)样本成绩属于第六组的有![]() 人,样本成绩属于第八组的有
人,样本成绩属于第八组的有![]() 人,
人,
从样本成绩属于第六组和第八组的所有学生中随机抽取2名,
基本事件总数![]() ,
,
他们的分差的绝对值小于10分包含的基本事件个数![]() ,
,
故他们的分差的绝对值小于10分的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是
是![]() 的两个非空子集,如果存在一个函数
的两个非空子集,如果存在一个函数![]() 满足:①
满足:① ![]() ;② 对任意
;② 对任意![]() ,当
,当![]() 时,恒有
时,恒有![]() ,那么称这两个集合为“
,那么称这两个集合为“![]() 到
到![]() 的保序同构”,以下集合对不是“
的保序同构”,以下集合对不是“![]() 到
到![]() 的保序同构”的是( )
的保序同构”的是( )
A.![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:实数![]() 满足不等式
满足不等式![]() ;
;
命题q:关于![]() 不等式
不等式![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)若命题![]() 为真命题,求实数
为真命题,求实数![]() 的取值范围;
的取值范围;
(2)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
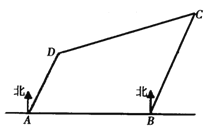
【题目】如图,有四座城市![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 在
在![]() 的正东方向,且与
的正东方向,且与![]() 相距
相距![]() ,
,![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ;
;![]() 在
在![]() 的北偏东
的北偏东![]() 方向,且与
方向,且与![]() 相距
相距![]() ,一架飞机从城市
,一架飞机从城市![]() 出发以
出发以![]() 的速度向城市
的速度向城市![]() 飞行,飞行了
飞行,飞行了![]() ,接到命令改变航向,飞向城市
,接到命令改变航向,飞向城市![]() ,此时飞机距离城市
,此时飞机距离城市![]() 有( )
有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() )的周期为
)的周期为![]() ,图象的一个对称中心为
,图象的一个对称中心为![]() 将函数
将函数![]() 图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移
图象上的所有点的横坐标伸长为原来的2倍(纵坐标不变),再将所有图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象.
的图象.
(1)求函数![]() 与
与![]() 的解析式;
的解析式;
(2)当![]() ,求实数
,求实数![]() 与正整数
与正整数![]() ,使
,使![]() 在
在![]() 恰有2019个零点.
恰有2019个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动制衣品牌为了成衣尺寸更精准,现选择15名志愿者,对其身高和臂展进行测量(单位:厘米),左图为选取的15名志愿者身高与臂展的折线图,右图为身高与臂展所对应的散点图,并求得其回归方程为![]() ,以下结论中不正确的为
,以下结论中不正确的为


A. 15名志愿者身高的极差小于臂展的极差
B. 15名志愿者身高和臂展成正相关关系,
C. 可估计身高为190厘米的人臂展大约为189.65厘米,
D. 身高相差10厘米的两人臂展都相差11.6厘米,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理中是演绎推理的为( )
A. 由金、银、铜、铁可导电,猜想:金属都可导电
B. 猜想数列![]() 的通项公式为
的通项公式为![]()
C. 半径为![]() 的圆的面积
的圆的面积![]() ,则单位圆的面积
,则单位圆的面积![]()
D. 由平面直角坐标系中圆的方程为![]() ,推测空间直角坐标系中球的方程为
,推测空间直角坐标系中球的方程为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com