
已知等差数列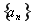 的公差大于0,且
的公差大于0,且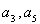 是方程
是方程 的两根,数列
的两根,数列 的前n项的和为
的前n项的和为 ,且
,且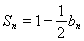 .
.
(1)求数列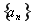 ,
, 的通项公式;
的通项公式;
(2)记 ,求证:
,求证: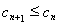 .
.
(1)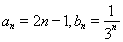 ; (2) 详见解析.
; (2) 详见解析.
【解析】
试题分析:(1) 求等差数列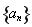 的通项公式,只需求出
的通项公式,只需求出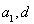 即可,因为
即可,因为 是方程
是方程 的两根,且数列
的两根,且数列 的公差
的公差 , 这样可求出
, 这样可求出 ,从而可得数列
,从而可得数列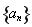 的通项公式,又因为数列
的通项公式,又因为数列 的前
的前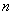 项和为
项和为 ,
, ,可利用
,可利用 得到递推关系,
得到递推关系, ,得出
,得出 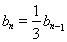 ,数列
,数列 是等比数列,根据等比数列的通项公式写出
是等比数列,根据等比数列的通项公式写出 ; (2) 记
; (2) 记 ,求证:
,求证: ,首先写出数列
,首先写出数列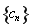 的通项公式,
的通项公式, , 要证明
, 要证明 ,可用作差比较法,只需证
,可用作差比较法,只需证 即可.
即可.
试题解析:(1)∵ 是方程
是方程 的两根,且数列
的两根,且数列 的公差d>0,
的公差d>0,
∴ ,公差
,公差
∴ 3分
3分
又当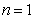 时,有
时,有 ,-所以
,-所以 ,
,
当
∴数列 是等比数列,
是等比数列,
∴ 6分
6分
(2)由(1)知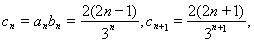 9分
9分
∴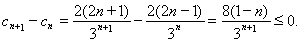
∴ 12分
12分
考点:数列与不等式的综合,等差数列的通项公式,等比数列的通项公式,等比数列的通项公式.


科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标2-3练习卷(解析版) 题型:解答题
如图,△ABC内接于⊙O,点D在OC的延长线上,sinB=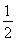 ,∠D=30°.
,∠D=30°.
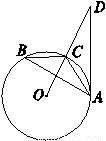
(1)求证:AD是⊙O的切线.
(2)若AC=6,求AD的长.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-3练习卷(解析版) 题型:解答题
如图,在△ABC中,延长BC到D,使CD=BC,取AB的中点F,连接FD交AC于点E.
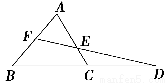
(1)求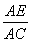 的值;
的值;
(2)若AB=a,FB=EC,求AC的长.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:解答题
如图,以梯形ABCD的对角线AC及腰AD为邻边作平行四边形ACED,DC的延长线交BE于点F,求证:EF=BF.
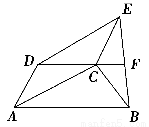
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高中数学人教A版选修4-1知能达标1-1练习卷(解析版) 题型:选择题
如图,已知AB∥CD∥EF,AF,BE相交于点O,若AO=OD=DF,BE=10 cm,则BO的长为 ( ).
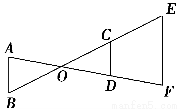
A.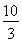 cm B.5 cm
cm B.5 cm
C.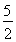 cm D.3 cm
cm D.3 cm
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西西安第一中学高三第二学期第二次模拟考试理科数学试卷(解析版) 题型:选择题
△ABC的三个内角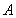 ,
,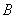 ,
,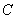 所对的边分别为
所对的边分别为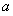 ,
,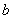 ,
,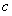 ,
,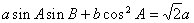 ,则
,则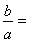 ( )
( )
A.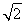 B.
B.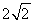 C.
C.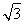 D.
D.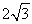
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com