
【题目】选修4﹣1:几何证明选讲
如图,AB为⊙O直径,直线CD与⊙O相切与E,AD垂直于CD于D,BC垂直于CD于C,EF垂直于F,连接AE,BE.证明:
(1)∠FEB=∠CEB;
(2)EF2=ADBC.
【答案】
(1)证明:∵直线CD与⊙O相切于E,∴∠CEB=∠EAB.
∵AB为⊙O的直径,∴∠AEB=90°.
∴∠EAB+∠EBA=90°.
∵EF⊥AB,∴∠FEB+∠EBF=90°.
∴∠FEB=∠EAB.
∴∠CEB=∠EAB.
(2)证明:∵BC⊥CD,∴∠ECB=90°=∠EFB,
又∠CEB=∠FEB,EB公用.
∴△CEB≌△FEB.
∴CB=FB.
同理可得△ADE≌△AFE,∴AD=AF.
在Rt△AEB中,∵EF⊥AB,∴EF2=AFFB.
∴EF2=ADCB.
【解析】(1)直线CD与⊙O相切于E,利用弦切角定理可得∠CEB=∠EAB.由AB为⊙O的直径,可得∠AEB=90°.又EF⊥AB,利用互余角的关系可得∠FEB=∠EAB,从而得证.(2)利用(1)的结论及∠ECB=90°=∠EFB和EB公用可得△CEB≌△FEB,于是CB=FB.同理可得△ADE≌△AFE,AD=AF.在Rt△AEB中,由EF⊥AB,利用射影定理可得EF2=AFFB.等量代换即可.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为D,且
的定义域为D,且![]() 同时满足以下条件:
同时满足以下条件:
①![]() 在D上是单调递增或单调递减函数;
在D上是单调递增或单调递减函数;
②存在闭区间![]()
![]() D(其中
D(其中![]() ),使得当
),使得当![]() 时,
时,![]() 的取值集合也是
的取值集合也是![]() .那么,我们称函数
.那么,我们称函数![]() (
(![]() )是闭函数.
)是闭函数.
(1)判断![]() 是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
是不是闭函数?若是,找出条件②中的区间;若不是,说明理由.
(2)若![]() 是闭函数,求实数
是闭函数,求实数![]() 的取值范围.
的取值范围.
(注:本题求解中涉及的函数单调性不用证明,直接指出是增函数还是减函数即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(选修4﹣1:几何证明选讲)
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ![]() ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆 ![]() =l (a>b>0)的焦距为2,离心率为
=l (a>b>0)的焦距为2,离心率为 ![]() ,椭圆的右顶点为A.
,椭圆的右顶点为A.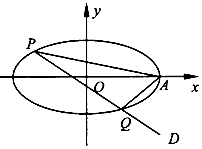
(1)求该椭圆的方程:
(2)过点D( ![]() ,﹣
,﹣ ![]() )作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
)作直线PQ交椭圆于两个不同点P,Q,求证:直线AP,AQ的
斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某工厂![]() 和
和![]() 两车间工人掌握某技术情况,现从这两车间工人中分别抽查
两车间工人掌握某技术情况,现从这两车间工人中分别抽查![]() 名和
名和![]() 名工人,经测试,将这
名工人,经测试,将这![]() 名工人的测试成绩编成的茎叶图。若成绩在
名工人的测试成绩编成的茎叶图。若成绩在![]() 以上(包括
以上(包括![]() )定义为“良好”,成绩在
)定义为“良好”,成绩在![]() 以下定义为“合格”。已知
以下定义为“合格”。已知![]() 车间工人的成绩的平均数为
车间工人的成绩的平均数为![]() ,
,![]() 车间工人的成绩的中位数为
车间工人的成绩的中位数为![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 车间工人的成绩的方差;
车间工人的成绩的方差;
(3)在这![]() 名工人中,用分层抽样的方法从 “良好”和“及格”中抽取
名工人中,用分层抽样的方法从 “良好”和“及格”中抽取![]() 人,再从这
人,再从这![]() 人中选
人中选![]() 人,求至少有一人为“良好”的概率。
人,求至少有一人为“良好”的概率。
(参考公式:方差![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com