
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(3)当![]() 时,记函数
时,记函数![]() 的导函数
的导函数![]() 的两个零点是
的两个零点是![]() 和
和![]() (
(![]() ),求证:
),求证:![]() .
.
【答案】(1)2x-y-2=0.(2)详见解析(3)详见解析
【解析】
试题分析:(1)由导数几何意义得曲线![]() 在
在![]() 处的切线斜率为f ′(1),所以先求导f ′(x)=2x -1+
处的切线斜率为f ′(1),所以先求导f ′(x)=2x -1+![]() ,再求斜率k=f ′(1)=2,最后由f(1)=0,利用点斜式可得切线方程:2x-y-2=0.(2)先求函数导数:f ′(x)=2ax-(2a+1)+
,再求斜率k=f ′(1)=2,最后由f(1)=0,利用点斜式可得切线方程:2x-y-2=0.(2)先求函数导数:f ′(x)=2ax-(2a+1)+![]() =
=![]() .再分类讨论导函数在定义区间上的零点:当a≤0时,一个零点1;当0<a时,两个零点
.再分类讨论导函数在定义区间上的零点:当a≤0时,一个零点1;当0<a时,两个零点![]() 和1;再比较两个零点大小,分三种情形.(3)本题实质研究函数
和1;再比较两个零点大小,分三种情形.(3)本题实质研究函数![]() 最小值.因为
最小值.因为![]() =(
=(![]() )-(bx1-bx2)+ln
)-(bx1-bx2)+ln![]() ,x1,x2是方程2x2-bx+1=0的两个根,所以bx=2x2+1,bx1-bx2=2(
,x1,x2是方程2x2-bx+1=0的两个根,所以bx=2x2+1,bx1-bx2=2(![]() );再由x1x2=
);再由x1x2=![]() 得
得![]()
![]() -
-![]() -ln(2
-ln(2![]() ),最后根据零点存在定理确定x2取值范围:x2∈(1,+∞),利用导数可得
),最后根据零点存在定理确定x2取值范围:x2∈(1,+∞),利用导数可得![]() 在区间(2,+∞)单调递增,即φ(t)>φ(2)=
在区间(2,+∞)单调递增,即φ(t)>φ(2)=![]() -ln2,
-ln2,
试题解析:(1)因为a=b=1,所以f(x)=x 2-x+lnx,
从而f ′(x)=2x -1+![]() .
.
因为f(1)=0,f ′(1)=2,故曲线y=f(x)在x=1处的切线方程为y-0=2(x-1),
即2x-y-2=0.
(2)因为b=2a+1,所以f(x)=ax2-(2a+1)x+lnx,
从而f ′(x)=2ax-(2a+1)+![]() =
=![]() =
=![]() ,x>0.
,x>0.
当a≤0时,x∈(0,1)时,f ′(x)>0,x∈(1,+∞)时,f ′(x)<0,
所以,f(x)在区间(0,1)上单调递增,在区间(1,+∞)上单调递减.
当0<a<![]() 时,
时,
由f ′(x)>0得0<x<1或x>![]() ,由f ′(x)<0得1<x<
,由f ′(x)<0得1<x<![]() ,
,
所以f(x)在区间(0,1)和区间(![]() ,+∞)上单调递增,在区间(1,
,+∞)上单调递增,在区间(1,![]() )上单调递减.
)上单调递减.
当a=![]() 时,
时,
因为f ′(x)≥0(当且仅当x=1时取等号),
所以f(x)在区间(0,+∞)上单调递增.
当a>![]() 时,
时,
由f ′(x)>0得0<x<![]() 或x>1,由f ′(x)<0得
或x>1,由f ′(x)<0得![]() <x<1,
<x<1,
所以f(x)在区间(0,![]() )和区间(1,+∞)上单调递增,在区间(
)和区间(1,+∞)上单调递增,在区间(![]() ,1)上单调递减.
,1)上单调递减.
(3)方法一:因为a=1,所以f(x)=x2-bx+lnx,从而f ′(x)=![]() (x>0).
(x>0).
由题意知,x1,x2是方程2x2-bx+1=0的两个根,故x1x2=![]() .
.
记g(x) =2x2-bx+1,因为b>3,所以g(![]() )=
)=![]() <0,g(1)=3-b<0,
<0,g(1)=3-b<0,
所以x1∈(0,![]() ),x2∈(1,+∞),且bxi=2
),x2∈(1,+∞),且bxi=2![]() +1 (i=1,2).
+1 (i=1,2).
f(x1)-f(x2)=(![]() )-(bx1-bx2)+ln
)-(bx1-bx2)+ln![]() =-(
=-(![]() )+ln
)+ln![]() .
.
因为x1x2=![]() ,所以f(x1)-f(x2)=
,所以f(x1)-f(x2)=![]() -
-![]() -ln(2
-ln(2![]() ),x2∈(1,+∞).
),x2∈(1,+∞).
令t=2![]() ∈(2,+∞),φ(t)=f(x1)-f(x2)=
∈(2,+∞),φ(t)=f(x1)-f(x2)=![]() -lnt.
-lnt.
因为φ′(t)=![]() ≥0,所以φ(t)在区间(2,+∞)单调递增,
≥0,所以φ(t)在区间(2,+∞)单调递增,
所以φ(t)>φ(2)=![]() -ln2,即f(x1)-f(x2)>
-ln2,即f(x1)-f(x2)>![]() -ln2.
-ln2.
方法二:因为a=1,所以f(x)=x2-bx+lnx,从而f ′(x)=![]() (x>0).
(x>0).
由题意知,x1,x2是方程2x2-bx+1=0的两个根.
记g(x) =2x2-bx+1,因为b>3,所以g(![]() )=
)=![]() <0,g(1)=3-b<0,
<0,g(1)=3-b<0,
所以x1∈(0,![]() ),x2∈(1,+∞),且f(x)在[x1,x2]上为减函数.
),x2∈(1,+∞),且f(x)在[x1,x2]上为减函数.
所以f(x1)-f(x2)>f(![]() )-f(1)=(
)-f(1)=(![]() -
-![]() +ln
+ln![]() )-(1-b)=-
)-(1-b)=-![]() +
+![]() -ln2.
-ln2.
因为b>3,故f(x1)-f(x2)>-![]() +
+![]() -ln2>
-ln2>![]() -ln2.
-ln2.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知a,b,c是![]() ABC中角A,B,C的对边,S是
ABC中角A,B,C的对边,S是![]() ABC的面积.若a2+c2=b2+ac,
ABC的面积.若a2+c2=b2+ac,
(I)求角B ; (II)若b=2,S=![]() ,判断三角形形状
,判断三角形形状
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. ![]() ,
, ![]() 为不共线向量,若
为不共线向量,若![]() ,则
,则![]()
B. 若![]() ,
, ![]() 为平面内两个不相等向量,则平面内任意向量
为平面内两个不相等向量,则平面内任意向量![]() 都可以表示为
都可以表示为![]()
C. 若![]() ,
, ![]() ,则
,则![]() 与
与![]() 不一定共线
不一定共线
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
⑴从区间![]() 内任取一个实数
内任取一个实数![]() ,设事件
,设事件![]() 表示“函数
表示“函数![]() 在区间
在区间![]() 上有两个不同的零点”,求事件
上有两个不同的零点”,求事件![]() 发生的概率;
发生的概率;
⑵若联系掷两次一颗均匀的骰子(骰子六个面上标注的点数分别为![]() )得到的点数分别为
)得到的点数分别为![]() 和
和![]() ,记事件
,记事件![]() 表示“
表示“![]() 在
在![]() 上恒成立”,求事件
上恒成立”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知坐标平面上点![]() 与两个定点
与两个定点![]() ,
, ![]() 的距离之比等于
的距离之比等于![]() .
.
(1)求点![]() 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;
(2)记(1)中的轨迹为![]() ,过点
,过点![]() 的直线
的直线![]() 被
被![]() 所截得的线段的长为
所截得的线段的长为![]() ,求直线
,求直线![]() 的方程
的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 恒过定点
恒过定点![]() ,圆
,圆![]() 经过点
经过点![]() 和点
和点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求定点![]() 的坐标;
的坐标;
(2)求圆![]() 的方程;
的方程;
(3)已知点![]() 为圆
为圆![]() 直径的一个端点,若另一个端点为点
直径的一个端点,若另一个端点为点![]() ,问:在
,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 为直角三角形,若存在,求出
为直角三角形,若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节进行社会实践,对![]() 岁的人群随机抽取
岁的人群随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低硕族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族的人数 | 占本组的频率 |
第一组 |
| 120 | 0.6 |
第二组 |
| 195 |
|
第三组 |
| 100 | 0.5 |
第四组 |
|
| 0.4 |
第五组 |
| 30 | 0.3 |
第六组 |
| 15 | 0.3 |
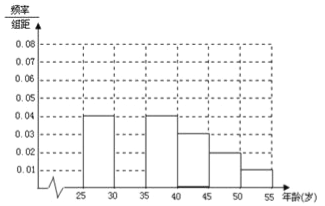
(1)补全频率分布直方图并求![]() 的值(直接写结果);
的值(直接写结果);
(2)从年龄段在![]() 的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在
的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中至少有1人年龄在![]() 岁的概率.
岁的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com