
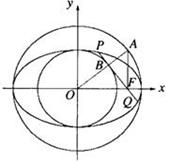
如图,以椭圆![]() 的中心
的中心![]() 为圆心,分别以
为圆心,分别以![]() 和
和![]() 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点![]() 作垂直于
作垂直于![]() 轴的直线交大圆于第一象限内的点
轴的直线交大圆于第一象限内的点![]() .连结
.连结![]() 交小圆于点
交小圆于点![]() .设直线
.设直线![]() 是小圆的切线.
是小圆的切线.
(1)证明![]() ,并求直线
,并求直线![]() 与
与![]() 轴的交点
轴的交点![]() 的坐标;
的坐标;
(2)设直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,证明
两点,证明![]() .
.

本小题主要考查椭圆的标准方程和几何性质、直线方程、平面向量、曲线和方程的关系等解析几何的基础知识和基本思想方法,考查推理及运算能力.
(Ⅰ)证明:由题设条件知,Rt△OFA∽Rt△OBF,故
![]() 即
即![]() .
.
因此,![]() 。
。
解:在Rt△OFA中,
![]()
于是,直线OA的斜率![]() .设直线BF的斜率为k,则
.设直线BF的斜率为k,则
![]()
这时,直线BF的方程为![]() (x-c),令x=0,则
(x-c),令x=0,则
![]()
所以直线BF与y轴的交点为M(0,a).
(Ⅱ)证明:由(Ⅰ),得直线BF的方程为y=kx+a,且
![]() ②
②
由已知,设P(x1,y1)、Q(x2,y2),则它们的坐标满足方程组
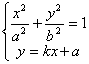 ③
③
由方程组③消去y,并整理得
![]() . ④
. ④
由①、②和④,
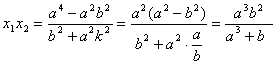
由方程组③消去x,并整理得
![]() ⑤
⑤
由式②和⑤,

综上,得到
![]() 。
。
注意到![]() ,得
,得
![]()
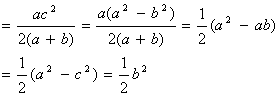


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
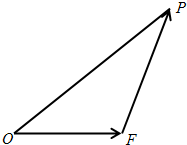 如图,设△OEP的面积为S,已知
如图,设△OEP的面积为S,已知| OF |
| FP |
| 1 |
| 2 |
| ||
| 2 |
| OF |
| FP |
| 3 |
| 4 |
| OF |
| OF |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年天津卷理)(14分)
如图,以椭圆![]() 的中心O为圆心,分别以
的中心O为圆心,分别以![]() 和
和![]() 为半径作大圆和小圆。过椭圆右焦点
为半径作大圆和小圆。过椭圆右焦点![]() 作垂直于
作垂直于![]() 轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。
轴的直线交大圆于第一象限内的点A。连结OA交小圆于点B。设直线BF是小圆的切线。

(I)证明![]() 并求直线BF与
并求直线BF与![]() 同的交点M的坐标;
同的交点M的坐标;
(II)设直线BF交椭圆P、Q两点,证明![]()
查看答案和解析>>
科目:高中数学 来源:2011年浙江省杭州市萧山区高考数学模拟试卷05(文科)(解析版) 题型:解答题
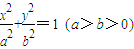 的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.
的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.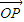 •
•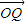 =
= b2.
b2.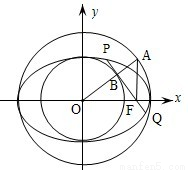
查看答案和解析>>
科目:高中数学 来源:2006年天津市高考数学试卷(理科)(解析版) 题型:解答题
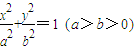 的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.
的中心O为圆心,分别以a和b为半径作大圆和小圆.过椭圆右焦点F(c,0)(c>b)作垂直于x轴的直线交大圆于第一象限内的点A.连接OA交小圆于点B.设直线BF是小圆的切线.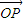 •
•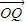 =
= b2.
b2.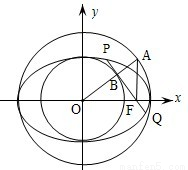
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com