练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某中学高一、高二、高三年级的学生人数之比依次为6：5：7，防疫站欲对该校学生进行身体健康调查，用分层抽样的方法从该校高中三个年级的学生中抽取容量为n的样本，样本中高三年级的学生有21人，则n等于（ ）

    A.35B.45C.54D.63

    【答案】C

    【解析】

    由某中学高一、高二、高三年级的学生人数之比为6：5：7，知高三年级学生的数量占总数的，再由分层抽样的方法从三个年级的学生中抽取一个容量为n的样本，高三年级被抽到的人数为21人，能求出n.

    解：∵某中学高一、高二、高三年级的学生人数之比为6：5：7，

    ∴高三年级学生的数量占总数的，

    ∵分层抽样的方法从三个年级的学生中抽取一个容量为n的样本，若已知高三年级被抽到的人数为21人，

    ∴n＝2154.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.（其中为自然对数的底数）

    （1）当时，是否存在唯一的的值，使得？并说明理由；

    （2）若存在，使得对任意的恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．（其中常数，是自然对数的底数）

    （1）若，求在上的极大值点；

    （2）（）证明在上单调递增；

    （）求关于的方程在上的实数解的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我国天文学和数学著作《周髀算经》中记载：一年有二十四个节气，每个节气的晷长损益相同（晷是按照日影测定时刻的仪器，晷长即为所测量影子的长度）．二十四节气及晷长变化如图所示，相邻两个节气晷长减少或增加的量相同，周而复始．已知每年冬至的晷长为一丈三尺五寸，夏至的晷长为一尺五寸（一丈等于十尺，一尺等于十寸），则说法不正确的是（ ）

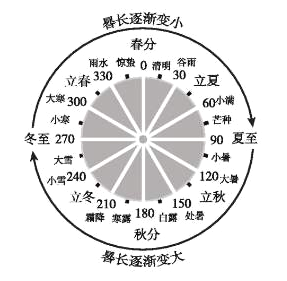
    A.相邻两个节气晷长减少或增加的量为一尺

    B.春分和秋分两个节气的晷长相同

    C.立冬的晷长为一丈五寸

    D.立春的晷长比立秋的晷长短

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数为自然对数的底数）．

    （1）求函数的值域；

    （2）若不等式对任意恒成立，求实数的取值范围；

    （3）证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设{an}是各项都为整数的等差数列，其前n项和为，是等比数列，且，，，.

    （1）求数列，的通项公式；

    （2）设cn＝log2b1+log2b2+log2b3+…+log2bn， .

    （i）求Tn；

    （ii）求证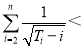：2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某投资人打算投资甲、乙两个项目，根据预测，甲、乙项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元，问投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯，由此催生了一批外卖点餐平台．已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调査送餐员的送餐收入，现从该平台随机抽取100名点外卖的用户进行统计，按送餐距离分类统计结果如表：

    送餐距离（千米）

    （0，1]

    （1，2]

    （2，3]

    （3，4]

    （4，5]

    频数

    15

    25

    25

    20

    15

    以这100名用户送餐距离位于各区间的频率代替送餐距离位于该区间的概率．

    （1）若某送餐员一天送餐的总距离为100千米，试估计该送餐员一天的送餐份数；（四舍五入精确到整数，且同一组中的数据用该组区间的中点值为代表）．

    （2）若该外卖平台给送餐员的送餐费用与送餐距离有关，规定2千米内为短距离，每份3元，2千米到4千米为中距离，每份7元，超过4千米为远距离，每份12元．记X为送餐员送一份外卖的收入（单位：元），求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】焦点在x轴上的椭圆C：经过点，椭圆C的离心率为．，是椭圆的左、右焦点，P为椭圆上任意点．

    （1）求椭圆的标准方程；

    （2）若点M为的中点（O为坐标原点），过M且平行于OP的直线l交椭圆C于A，B两点，是否存在实数，使得；若存在，请求出的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案