
【题目】已知函数![]() .
.
(Ⅰ)证明: 当![]() 时,
时, ![]() .
.
(Ⅱ)证明: 当![]() 时,
时, ![]() .
.
【答案】(1)详见解析;(Ⅱ)详见解析.
【解析】试题分析:
(Ⅰ)由不等式的特征构造函数![]() ,结合函数的单调性求得函数的最大值,据此即可证得题中的结论:
,结合函数的单调性求得函数的最大值,据此即可证得题中的结论: ![]() .
.
(Ⅱ)结合(I)的结论构造函数![]() ,研究该函数的性质即可证得当
,研究该函数的性质即可证得当![]() 时,
时, ![]() .
.
试题解析:
(Ⅰ)证明: 要证![]() , 也即证
, 也即证![]() .
.
令![]() , 则
, 则![]() . 令
. 令![]() , 则
, 则![]() . 因此, 当
. 因此, 当![]() 时, 有
时, 有![]() , 故
, 故![]() 在
在![]() 上单调递减; 当
上单调递减; 当![]() 时, 有
时, 有![]() , 故
, 故![]() 在
在![]() 上单调递增.
上单调递增.
所以, ![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
又![]() ,
, ![]() . 故
. 故![]() 成立, 即
成立, 即![]() 成立. 原命题得证.
成立. 原命题得证.
(Ⅱ) 证明: 由 (I) 得: 当![]() 时,
时, ![]()
令![]() , 则
, 则
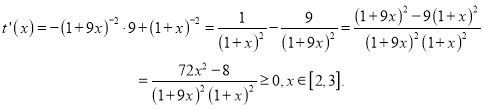
所以, ![]() 在
在![]() 上单调递增,即
上单调递增,即![]()
所以![]()
![]() 得证.
得证.
下证![]() .
.
即证![]()
令![]() 则
则![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
所以, ![]() ,得证.
,得证.
另证:要证![]() ,即证
,即证![]() ,
,
令![]() 在
在![]() 上递增,所以
上递增,所以![]() 得证.
得证.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】为了了解某地区心肺疾病是否与性别有关,在某医院随机地对入院
的50人进行了问卷调查,得到了如下的![]() 列联表:
列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 | 20 | 5 | 25 |
女 | 10 | 15 | 25 |
合计 | 30 | 20 | 50 |
(1)用分层抽样的方法在患心肺疾病的人群中抽取6人,其中男性抽多少人?
(2)在上述抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,判断是否有
,判断是否有![]() 的把握认为
的把握认为
患心肺疾病与性别有关?
右面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 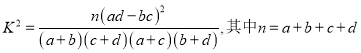 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an},{bn}中,a1=2,b1=4,且an,bn,an+1成等差数列,bn,an+1,bn+1成等比数列{n∈N+}.
求a2,a3,a4及b2,b3,b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据某市地产数据研究的数据显示,2016年该市新建住宅销售均价走势如下图所示,为抑制房价过快上涨,政府从8月采取宏观调控措施,10月份开始房价得到很好的抑制.
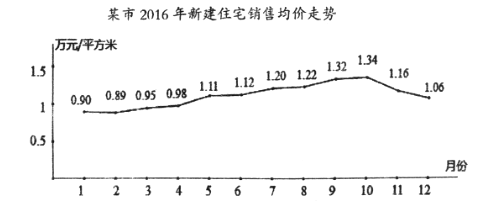
(1)地产数据研究院发现,3月至7月的各月均价![]() (万元/平方米)与月份
(万元/平方米)与月份![]() 之间具有较强的线性相关关系,试建立
之间具有较强的线性相关关系,试建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
的回归方程(系数精确到0.01);政府若不调控,依此相关关系预测第12月份该市新建住宅销售均价;
(2)地产数据研究院在2016年的12个月份中,随机抽取三个月的数据作样本分析,若关注所抽三个月份的所属季度,记不同季度的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据: ![]() ,
, ![]() ,
, ![]() ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
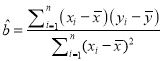 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com