
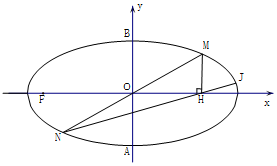
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形.分析 (1)由椭圆左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形,列出方程组,求出a,b,由此能求出椭圆C的方程.
(2)设M(x0,y0),则由条件,知x0>0,y0>0,且N(-x0,-y0),H(x0,0).推导出$M(\sqrt{2},\;\;\frac{{\sqrt{2}}}{2}\;),N(-\sqrt{2},\;\;-\frac{{\sqrt{2}}}{2}\;),H(\sqrt{2},\;\;0\;)$,进而求得直线NH的方程:$x-4y-\sqrt{2}=0$.由$\left\{\begin{array}{l}x-4y-\sqrt{2}=0\\ \;\;\frac{x^2}{4}+{y^2}=1\end{array}\right.$$求得\;J(\frac{7}{5}\sqrt{2},\;\;\frac{1}{10}\sqrt{2})$.再求出线段HJ的中点坐标,由此能求出以线段NJ为直径的圆的方程.
(3)当直线l1的斜率为0时,${S_{△PQR}}=2\sqrt{3}$.当直线l1的斜率存在且不为0时,设其方程为y=kx-1(k≠0),利用点到直线距离公式、弦长公式、直线垂直、三角形面积公式,结合已知条件能求出结果.
解答 解:(1)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左焦点为F,短轴的两个端点分别为A、B,且|AB|=2,△ABF为等边三角形.
∴由题意,得:$\left\{\begin{array}{l}\;2b=2\\ \;\;\;\;c=\sqrt{3}\;b\\ \;\;{b^2}+{c^2}={a^2},\;\end{array}\right.$$解得\;\left\{\begin{array}{l}\;a=2\\ \;b=1\\ c=\sqrt{3}.\end{array}\right.$,
∴椭圆C的方程为$\frac{x^2}{4}+{y^2}=1$.
(2)设M(x0,y0),则由条件,知x0>0,y0>0,且N(-x0,-y0),H(x0,0).
从而$\overrightarrow{HM}=(0,\;\;{y_0}),\overrightarrow{HN}=(-{x_0},\;\;-{y_0})$.
于是由$\overrightarrow{HM}•\overrightarrow{HN}=(0,\;\;{y_0})•(-{x_0},\;\;-{y_0})=-{y_0}^2=-\frac{1}{2},\;及\;{y_0}>0,得\;{y_0}=\frac{{\sqrt{2}}}{2}$.
再由点M在椭圆C上,得$\frac{{{x_0}^2}}{4}+{y_0}^2=1,\;\;求得\;{x_0}=\sqrt{2}$.
所以$M(\sqrt{2},\;\;\frac{{\sqrt{2}}}{2}\;),N(-\sqrt{2},\;\;-\frac{{\sqrt{2}}}{2}\;),H(\sqrt{2},\;\;0\;)$,
进而求得直线NH的方程:$x-4y-\sqrt{2}=0$.
由$\left\{\begin{array}{l}x-4y-\sqrt{2}=0\\ \;\;\frac{x^2}{4}+{y^2}=1\end{array}\right.$$求得\;J(\frac{7}{5}\sqrt{2},\;\;\frac{1}{10}\sqrt{2})$.
进而$|{\;NJ}|=\sqrt{{{(\frac{7}{5}\sqrt{2}+\sqrt{2})}^2}+{{(\frac{1}{10}\sqrt{2}+\frac{1}{2}\sqrt{2})}^2}}=\frac{3}{5}\sqrt{34},线段\;NJ\;的中点坐标为(\frac{1}{5}\sqrt{2},\;\;-\frac{1}{5}\sqrt{2})$.
∴以线段NJ为直径的圆的方程为:${(x-\frac{1}{5}\sqrt{2})^2}\;+{(y+\frac{1}{5}\sqrt{2})^2}=\frac{153}{50}$.
(3)当直线l1的斜率不存在时,直线l2与椭圆C相切于点A,不合题意,
当直线l1的斜率为0时,由题意得${S_{△PQR}}=2\sqrt{3}$.
当直线l1的斜率存在且不为0时,设其方程为y=kx-1(k≠0),
则点O到直线l1的距 离为$d=\frac{1}{{\sqrt{{k^2}+1}}}$,从而由几何意义,得$|{PQ}|=2\sqrt{4-{d^2}}=2\sqrt{\frac{{4{k^2}+3}}{{{k^2}+1}}}$,
由于l2⊥l1,故直线l2的方程为$y=-\frac{1}{k}x-1$,由题意得它与椭圆C的交点R的坐标为 $({-\frac{8k}{{{k^2}+4}},-\frac{{{k^2}-4}}{{{k^2}+4}}})$,
于是$|{AR}|=\sqrt{{{({-\frac{8k}{{{k^2}+4}}})}^2}+{{({-\frac{{{k^2}-4}}{{{k^2}+4}}+1})}^2}}=\frac{{8\sqrt{{k^2}+1}}}{{{k^2}+4}}$.
$故\;{S_{△PQR}}=\frac{1}{2}|{PQ}|•|{AR}|=\frac{{8\sqrt{4{k^2}+3}}}{{{k^2}+4}}$,
$令u=\sqrt{4{k^2}+3}>\sqrt{3},则$${S_{△PQR}}=\frac{32u}{{{u^2}+13}}=\frac{32}{{u+\frac{13}{u}}}≤\frac{16}{13}\sqrt{13}$,
当且仅当$u=\sqrt{13}(>\sqrt{3}),\;即\;k=±\frac{{\sqrt{10}}}{2}$时,上式取等号.
∵$\frac{16}{13}\sqrt{13}>2\sqrt{3}$,故当$k=±\frac{{\sqrt{10}}}{2}$时,${({{S_{△PQR}}})_{max}}=\frac{16}{13}\sqrt{13}$,
此时直线l1的方程为:$y=±\frac{{\sqrt{10}}}{2}x-1$.(也可写成 $±\sqrt{10}x+2y+2=0$.)
点评 本题考查椭圆方程的求法,考查圆的方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意椭圆、圆、直线方程、点到直线距离公式、弦长公式、直线垂直、三角形面积公式、中点坐标公式等知识点的灵活运用运用.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
 如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )
如图是求样本x1、x2、…x10平均数$\overline{x}$的程序框图,图中空白框中应填入的内容为( )| A. | S=S+xn | B. | S=S+$\frac{{x}_{n}}{n}$ | C. | S=S+n | D. | S=S+$\frac{{x}_{n}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )
刘徽的《九章算术注》中有这样的记载:“邪解立方有两堑堵,邪解堑堵,其一为阳马,一为鳖臑,阳马居二,鳖臑居一,不易之率也.”意思是说:把一块立方体沿斜线分成相同的两块,这两块叫做堑堵,再把一块堑堵沿斜线分成两块,大的叫阳马,小的叫鳖臑,两者体积比为2:1,这个比率是不变的,如图是一个阳马的三视图,则其表面积为( )| A. | 2 | B. | 2+$\sqrt{2}$ | C. | 3+$\sqrt{3}$ | D. | 3+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 单调递减的 | B. | 单调递增的 | C. | 先增后减的 | D. | 先减后增的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com